
【题目】探究题:
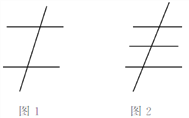
(1)如图1,两条水平的直线被一条竖直的直线所截,同位角有__________对,内错角有__________对,同旁内角有__________对;
(2)如图2,三条水平的直线被一条竖直的直线所截,同位角有__________对,内错角有__________对,同旁内角有__________对;
(3)根据以上探究的结果,n(n为大于1的整数)条水平直线被一条竖直直线所截,同位角有__________对,内错角有__________对,同旁内角有__________对.(用含n的式子表示)
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。
根据以上信息,解答下列问题:
(1)设租车时间为 ![]() 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为 ![]() 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为 ![]() 元,分别求出
元,分别求出 ![]() ,
, ![]() 关于
关于 ![]() 的函数表达式;
的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正整数能表示为两个连续奇数的平方差,那么称这个正整数为“奇特数”.例如:
![]() ,
,![]() ,
,![]() ;则
;则![]() 、
、![]() 、
、![]() 这三个数都是奇特数.
这三个数都是奇特数.
(1)![]() 和
和![]() 这两个数是奇特数吗?若是,表示成两个连续奇数的平方差形式.
这两个数是奇特数吗?若是,表示成两个连续奇数的平方差形式.
(2)设两个连续奇数是![]() 和
和![]() (其中
(其中![]() 取正整数),由这两个连续奇数构造的奇特数是
取正整数),由这两个连续奇数构造的奇特数是![]() 的倍数吗?为什么?
的倍数吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在AB上.
(1)试找出∠1,∠2,∠3之间的关系并说出理由;
(2)如果点P在A,B两点之间运动,问∠1,∠2,∠3之间的关系是否发生变化?
(3)如果点P在A,B两点外侧运动,试探究∠1,∠2,∠3之间的关系(点P和A,B不重合).

查看答案和解析>>
科目:初中数学 来源: 题型:
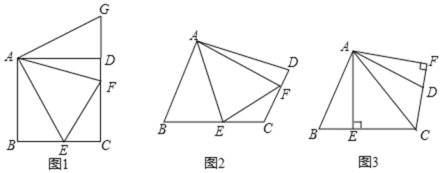
【题目】(1)如图 1,四边形 ABCD 中,∠BAD=∠ADC=∠CBA=90°,AB=AD,点 E、F 分别在四边形 ABCD 的边 BC、CD 上,∠EAF=45°,点 G 在 CD 的延长线上,BE=DG,连接 AG,求证:EF=BE+FD.
(2)如图 2,四边形 ABCD 中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点 E、F 分别在边BC、CD 上,则当∠BAD=2∠EAF 时,仍有 EF=BE+FD 成立吗?说明理由.
(3)如图 3,四边形 ABCD 中,∠BAD≠90°,AB=AD,AC 平分∠BCD,AE⊥BC 于 E,AF⊥CD 交 CD 延长线于 F,若 BC=9,CD=4,则 CE= .(不需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,补充条件后仍不一定能保证△ABC≌△A′B′C′,则补充的这个条件是( )

A. BC=B′C′ B. ∠A=∠A′ C. AC=A′C′ D. ∠C=∠C′
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,若△ABC和△ADE为等边三角形,M,N分别为EB,CD的中点,易证:CD=BE,△AMN是等边三角形: 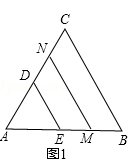
(1)当把△ADE绕点A旋转到图2的位置时,CD=BE吗?若相等请证明,若不等于请说明理由; 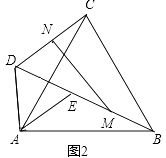
(2)当把△ADE绕点A旋转到图3的位置时,△AMN还是等边三角形吗?若是请证明,若不是,请说明理由(可用第一问结论). 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中.
(1)把△ABC平移至点A′的位置,使点A与点A′对应,画出平移后得到的△A′B′C′;
(2)△A′B′C′可以看成是把△ABC如何平移得到的?
(3)写出图中与线段AA′平行且相等的线段(可用字母表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
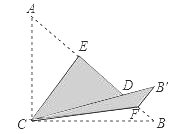
【题目】如图,Rt△ABC中,∠ACB=90°,![]() ,
,![]() ,将边
,将边![]() 沿
沿![]() 翻折,使点
翻折,使点![]() 落在
落在![]() 上的点
上的点![]() 处;再将边
处;再将边![]() 沿
沿![]() 翻折,使点
翻折,使点![]() 落在
落在![]() 的延长线上的点
的延长线上的点![]() 处,两条折痕与斜边
处,两条折痕与斜边![]() 分别交于点
分别交于点![]() 、
、![]() ,则线段
,则线段![]() 的长为( )
的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com