
【题目】如图,扇形AOD中,∠AOD=90°,OA=6,点P为弧AD上任意一点(不与点A和D重合),PQ⊥OD于点Q,点I为△OPQ的内心,过O、I和D三点的圆的半径为r,则当点P在弧AD上运动时,求r的值.
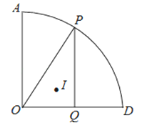
【答案】r的值为3![]() .
.
【解析】
连OI,PI,DI,由△OPH的内心为I,可得到∠PIO=180°-∠IPO-∠IOP=180°-![]()
(∠HOP+∠OPH)=135°,并且易证△OPI≌△ODI,得到∠DIO=∠PIO=135°,所以点I在以OD为弦,并且所对的圆周角为135°的一段劣弧上;过D、I、O三点作⊙O′,如图,连O′D,O′O,在优弧AO取点P′,连P′D,P′O,可得∠DP′O=180°-135°=45°,得∠DO′O=90°,O′O=3![]() .
.
解:如图,连OI,PI,DI,
∵△OPH的内心为I,
∴∠IOP=∠IOD,∠IPO=∠IPH,
∴∠PIO=180°﹣∠IPO﹣∠IOP=180°﹣![]() (∠HOP+∠OPH),
(∠HOP+∠OPH),
而PH⊥OD,即∠PHO=90°,
∴∠PIO=180°﹣![]() (∠HOP+∠OPH)=180°﹣
(∠HOP+∠OPH)=180°﹣![]() (180°﹣90°)=135°,
(180°﹣90°)=135°,
在△OPI和△ODI中,
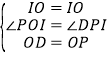 ,
,
∴△OPI≌△ODI(SAS),
∴∠DIO=∠PIO=135°,
所以点I在以OD为弦,并且所对的圆周角为135°的一段劣弧上;
过D、I、O三点作⊙O′,如图,连O′D,O′O,
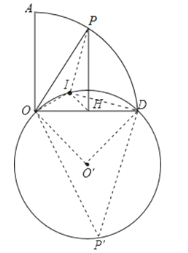
在优弧DO取点P′,连P′D,P′O,
∵∠DIO=135°,
∴∠DP′O=180°﹣135°=45°,
∴∠DO′O=90°,而OD=6,
∴OO′=DO′=3![]() ,
,
∴r的值为3![]() .
.


科目:初中数学 来源: 题型:
【题目】某区在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的50个家庭去年月平均用水量(单位:吨),并将调查数据进行如下整理:
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
频数分布表
分组 | 划记 | 频数 |
2.0<x≤3.5 | 正正 | 11 |
3.5<x≤5.0 |
| 19 |
5.0<x≤6.5 | ||
6.5<x≤8.0 | ||
8.0<x≤9.5 |
| 2 |
合计 | 50 |
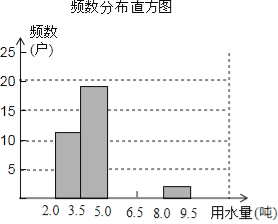
(1)把上面频数分布表和频数分布直方图补充完整;
(2)从直方图中你能得到什么信息?(写出两条即可);
(3)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费,若要使60%的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90![]() ,AB=AC.点D为直线BC上一动点(点D不与点B、C重合),以AD为直角边在AD右侧作等腰直角三角形ADE,使
,AB=AC.点D为直线BC上一动点(点D不与点B、C重合),以AD为直角边在AD右侧作等腰直角三角形ADE,使![]() DAE=90
DAE=90![]() ,连结CE.
,连结CE.
探究:如图①,当点D在线段BC上时,证明BC=CE+CD.
应用:在探究的条件下,若AB=![]() ,CD=1,则△DCE的周长为_______.
,CD=1,则△DCE的周长为_______.
拓展:(1)如图②,当点D在线段CB的延长线上时,BC、CD、CE之间的数量关系为_______.
(2)如图③,当点D在线段BC的延长线上时,BC、CD、CE之间的数量关系为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=120°,OP平分∠AOB,且OP=1.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( )
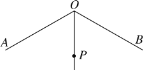
A.1个B.2个C.3个D.无数个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划购买A,B两种型号的机器人搬运材料.已知A型机器人比B型机器人每小时多搬运30kg材料,且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同.
(1)求A,B两种型号的机器人每小时分别搬运多少材料;
(2)该公司计划采购A,B两种型号的机器人共20台,要求每小时搬运材料不得少于2800kg,则至少购进A型机器人多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 y=ax2+bx+c(a≠0),过(1,y1)(2,y2).
①若 y1>0 时,则 a+b+c>0
②若 a=b 时,则 y1<y2
③若 y1<0,y2>0,且 a+b<0,则 a>0
④若 b=2a﹣1,c=a﹣3,且 y1>0,则抛物线的顶点一定在第三象限上述四个判断正确的有( )个.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某同学想测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同一时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上的影长为21米,留在墙上的影高为2米,求旗杆的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市正在开展“食品安全城市”创建活动,为了解学生对食品安全知识的了解情况,学校随机抽取了部分学生进行问卷调查,将调查结果按照“![]() 非常了解、
非常了解、![]() 了解、
了解、![]() 了解较少、
了解较少、![]() 不了解”四类分别进行统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题:
不了解”四类分别进行统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题:
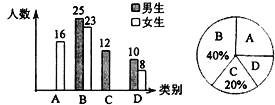
(1)此次共调查了__________名学生;
(2)扇形统计图中![]() 所在扇形的圆心角为__________°;
所在扇形的圆心角为__________°;
(3)将上面的条形统计图补充完整;
(4)若该校共有1600名学生,请你估计对食品安全知识“非常了解”的学生的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com