
ЁОЬтФПЁПавИЃДхдкЭЦНјУРРіЯчДхНЈЩшжаЃЌОіЖЈНЈЩшавИЃЙуГЁЃЌМЦЛЎЦЬЩшЯрЭЌДѓаЁЁЂЙцИёЕФКьЩЋКЭРЖЩЋЕизЉЃЌОЙ§ЕїВщЃЌЛёШЁаХЯЂШчЯТБэЃК
РрБ№ | ЙКТђЪ§СПЕЭгк500Пщ | ЙКТђЪ§СПВЛЕЭгк500Пщ |
КьЩЋЕизЉ | дМлЯњЪл | вдАЫелЯњЪл |
РЖЩЋЕизЉ | дМлЯњЪл | вдОХелЯњЪл |
ШєЙКТђКьЩЋЕизЉ400ПщЃЌРЖЩЋЕизЉ600ПщЃЌашИЖПю8600дЊЃЛШєЙКТђКьЩЋЕизЉ1000ПщЃЌРЖЩЋЕизЉ350ПщЃЌашИЖПю9900дЊЃЎ
ЃЈ1ЃЉКьЩЋЕизЉКЭРЖЩЋЕизЉЕФЕЅМлИїЖрЩйдЊЃП
ЃЈ2ЃЉОЙ§ВтЫуЃЌашвЊЙКжУЕизЉ1200ПщЃЌЦфжаРЖЩЋЕизЉЕФЪ§СПВЛЩйгкКьЩЋЕизЉЕФвЛАыЃЌВЂЧвВЛГЌЙ§600ПщЃЌШчКЮЙКТђИЖПюзюЩйЃПзюЩйЪЧЖрЩйдЊЃПЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉКьЩЋЕизЉУППщ8дЊЃЌРЖЩЋЕизЉУППщ10дЊЃЛЃЈ2ЃЉЙКТђРЖЩЋЕизЉ700ПщЃЌКьЩЋЕизЉ500ПщЃЌЗбгУзюЩйЃЌзюЩйЗбгУЮЊ8980дЊЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтвтНсКЯБэИёжаЪ§ОнЃЌЙКТђКьЩЋЕизЉ4000ПщЃЌРЖЩЋЕизЉ6000ПщЃЌашИЖПю86000дЊЃЛЙКТђКьЩЋЕизЉ10000ПщЃЌРЖЩЋЕизЉ3500ПщЃЌашИЖПю99000дЊЃЌЗжБ№ЕУГіЗНГЬЕУГіД№АИЃЛ
ЃЈ2ЃЉРћгУвбжЊЕУГіxЕФШЁжЕЗЖЮЇЃЌдйРћгУвЛДЮКЏЪ§діМѕадЕУГіД№АИЃЎ
ЃЈ1ЃЉЩшКьЩЋЕизЉУППщxдЊЃЌРЖЩЋЕизЉУППщyдЊЃЌгЩЬтвтПЩЕУЃК
![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
Д№ЃККьЩЋЕизЉУППщ8дЊЃЌРЖЩЋЕизЉУППщ10дЊЃЛ
ЃЈ2ЃЉЩшЙКжУРЖЩЋЕизЉaПщЃЌдђЙКжУКьЩЋЕизЉЃЈ1200ЉaЃЉПщЃЌЫљашЕФзмЗбгУЮЊyдЊЃЌ
гЩЬтвтПЩЕУЃК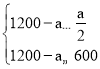 ЃЌ
ЃЌ
НтЕУЃК600ЁмaЁм800ЃЌ
ЕБ600ЁмaЃМ700ЪБЃЌ
yЃН8aЁС0.8+0.9ЁС10ЃЈ1200ЉaЃЉЃН10800Љ2.6aЃЌ
ЕБaЃН700ЪБyгазюаЁжЕЮЊЃК10800Љ2.6ЁС700ЃН8980ЃЌ
ЕБ700ЃМxЁм800ЪБЃЌyЃН8aЁС0.8+10ЃЈ1200ЉaЃЉЃНЉ3.6a+12000ЃЌ
ЕБaЃН800ЪБЃЌyгазюаЁжЕЮЊЃКЉ3.6ЁС800+12000ЃН9120ЃЌ
Ёп9120ЃМ9180ЃЌ
ЁрЙКТђРЖЩЋЕизЉ700ПщЃЌКьЩЋЕизЉ500ПщЃЌЗбгУзюЩйЃЌзюЩйЗбгУЮЊ8980дЊЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯўЖЋдкНтвЛдЊЖўДЮЗНГЬЪБЃЌЗЂЯжгаетбљвЛжжНтЗЈЃК
ШчЃКНтЗНГЬ![]() .
.
НтЃКдЗНГЬПЩБфаЮЃЌЕУ
![]() .
.
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]()
жБНгПЊЦНЗНВЂећРэЃЌЕУ![]() ЃЌ
ЃЌ![]() .
.
ЮвУЧГЦЯўЖЋетжжНтЗЈЮЊЁАЦНОљЪ§ЗЈЁБЃЎ
ЃЈ1ЃЉЯТУцЪЧЯўЖЋгУЁАЦНОљЪ§ЗЈЁБНтЗНГЬ![]() ЪБаДЕФНтЬтЙ§ГЬЃЎ
ЪБаДЕФНтЬтЙ§ГЬЃЎ
![]() .
.
![]() ЃЌ
ЃЌ
![]() .
.
жБНгПЊЦНЗНВЂећРэЃЌЕУ![]() ЃЌ
ЃЌ![]() .
.
ЩЯЪіЙ§ГЬжаЕФЁАЁѕЁБЃЌЁАЁ№ЁБЃЌЁАЁюЁБЃЌЁАЁшЁББэЪОЕФЪ§ЗжБ№ЮЊ________ЃЌ________ЃЌ________ЃЌ________.
ЃЈ2ЃЉЧыгУЁАЦНОљЪ§ЗЈЁБНтЗНГЬЃК![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєХзЮяЯпLЃКy=ax2+bx+cЃЈaЃЌbЃЌcЪЧГЃЪ§ЃЌabcЁй0ЃЉгыжБЯпlЖМОЙ§yжсЩЯЕФЭЌвЛЕуЃЌЧвХзЮяЯпLЕФЖЅЕудкжБЯпlЩЯЃЌдђГЦДЮХзЮяЯпLгыжБЯпlОпгаЁАвЛДјвЛТЗЁБЙиЯЕЃЌВЂЧвНЋжБЯпlНазіХзЮяЯпLЕФЁАТЗЯпЁБЃЌХзЮяЯпLНазіжБЯпlЕФЁАДјЯпЁБЃЎ
ЃЈ1ЃЉШєЁАТЗЯпЁБlЕФБэДяЪНЮЊy=2xЉ4ЃЌЫќЕФЁАДјЯпЁБLЕФЖЅЕуЕФКсзјБъЮЊЉ1ЃЌЧѓЁАДјЯпЁБLЕФБэДяЪНЃЛ
ЃЈ2ЃЉШчЙћХзЮяЯпy=mx2Љ2mx+mЉ1гыжБЯпy=nx+1ОпгаЁАвЛДјвЛТЗЁБЙиЯЕЃЌЧѓmЃЌnЕФжЕЃЛ
ЃЈ3ЃЉЩшЃЈ2ЃЉжаЕФЁАДјЯпЁБLгыЫќЕФЁАТЗЯпЁБlдкyжсЩЯЕФНЛЕуЮЊAЃЎвбжЊЕуPЮЊЁАДјЯпЁБLЩЯЕФЕуЃЌЕБвдЕуPЮЊдВаФЕФдВгыЁАТЗЯпЁБlЯрЧагкЕуAЪБЃЌЧѓГіЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАЪ§бЇРДдДгкЩњЛюЃЌгждЫгУгкЩњЛюЁБВмРЯЪІЮЊСЫСЫНтЫљНЬАрМЖбЇЩњРћгУЪ§бЇжЊЪЖНтОіЪЕМЪЮЪЬтЕФФмСІЃЌБржЦШєИЩЮЪЬтЖдШЋАрбЇЩњНјааСЫвЛДЮВтЪдЃЌВЂНЋВтЪдНсЙћЗжГЩЫФРрЃЌAЬиБ№ЧПЃКBЃКЧПЃЛCЃКвЛАуЃКDНЯШѕвдЯТЪЧгЩЕїВщВтЪдНсЙћЛцжЦЕФСНЗљВЛЭъећЕФЭГМЦЭМЃЌЧыФуИљОнЭГМЦЭМЭъГЩвдЯТНтД№ЃЎ
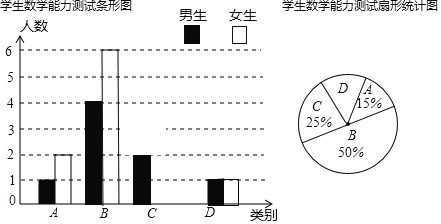
ЃЈ1ЃЉВмРЯЪІЕФАрМЖЙВгаЁЁ ЁЁУћбЇЩњЃЛ
ЃЈ2ЃЉНЋЯТУцЬѕаЮЭГМЦЭМЕФCРрВПЗжВЙГфЭъећЃЛ
ЃЈ3ЃЉЩШаЮЭГМЦЭМжаЃЌDРрЖдгІЕФдВаФНЧЮЊЖрЩйЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПРћгУШчЭМ1ЕФЖўЮЌТыПЩвдНјааЩэЗнЪЖБ№.ФГаЃНЈСЂСЫвЛИіЩэЗнЪЖБ№ЯЕЭГЃЌЭМ2ЪЧФГИібЇЩњЕФЪЖБ№ЭМАИЃЌКкЩЋаЁе§ЗНаЮБэЪО1ЃЌАзЩЋаЁе§ЗНаЮБэЪО0.НЋЕквЛааЪ§зжДгзѓЕНгввРДЮМЧЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌФЧУДПЩвдзЊЛЛЮЊИУЩњЫљдкАрМЖађКХЃЌЦфађКХЮЊ
ЃЌФЧУДПЩвдзЊЛЛЮЊИУЩњЫљдкАрМЖађКХЃЌЦфађКХЮЊ![]() .ШчЭМ2ЕквЛааЪ§зжДгзѓЕНгввРДЮЮЊ0ЃЌ1ЃЌ0ЃЌ1ЃЌађКХЮЊ
.ШчЭМ2ЕквЛааЪ§зжДгзѓЕНгввРДЮЮЊ0ЃЌ1ЃЌ0ЃЌ1ЃЌађКХЮЊ![]() ЃЌБэЪОИУЩњЮЊ5АрбЇЩњ.БэЪО6АрбЇЩњЕФЪЖБ№ЭМАИЪЧЃЈ ЃЉ
ЃЌБэЪОИУЩњЮЊ5АрбЇЩњ.БэЪО6АрбЇЩњЕФЪЖБ№ЭМАИЪЧЃЈ ЃЉ


A.  B.
B.  C.
C.  D.
D. 
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдквЛжЛВЛЭИУїЕФДќзгжазАга1ИіКьЩЋаЁЧђЃЌ2ИіЛЦЩЋаЁЧђКЭШєИЩИіКкЩЋаЁЧђЃЌетаЉаЁЧђГ§беЩЋвдЭтЖМвЛбљЃЎвбжЊДгДќжаШЮвтУўГі1ИіКьЩЋаЁЧђЕФИХТЪЪЧ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉДќжаКкЩЋаЁЧђЕФЪ§СПЪЧ ИіЃЛ
ЃЈ2ЃЉШєДгДќжаЫцЛњУўГі1ИіаЁЧђЃЌМЧТМКУбеЩЋКѓЗХЛиДќжаВЂНСдШЃЌдйДгДќжаШЮвтУўГі1ИіаЁЧђЃЌЧѓСНДЮУўГіЕФЖМЪЧЛЦЩЋаЁЧђЕФИХТЪЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
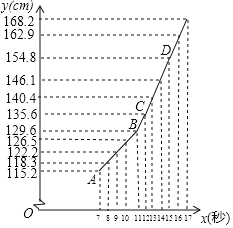
ЁОЬтФПЁПЪ§бЇаЫШЄаЁзщЮЊСЫбаОПжааЁбЇФаЩњЩэИпyЃЈcmЃЉКЭФъСфxЃЈЫъЃЉЕФЙиЯЕЃЌДгФГЪаЙйЭјЩЯЕУЕНСЫИУЪа2017ФъЭГМЦЕФжааЁбЇФаЩњИїФъСфзщЕФЦНОљЩэИпЃЌМћЯТБэЃКШчЭМвбОдкжБНЧзјБъЯЕжаУшГіСЫБэжаЪ§ОнЖдгІЕФЕуЃЌВЂЗЂЯжЧА5ИіЕуДѓжТЮЛгкжБЯпABЩЯЃЌКѓ7ИіЕуДѓжТЮЛгкжБЯпCDЩЯЃЎ
ФъСфзщx | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
ФаЩњЦНОљЩэИпy | 115.2 | 118.3 | 122.2 | 126.5 | 129.6 | 135.6 | 140.4 | 146.1 | 154.8 | 162.9 | 168.2 |
ЃЈ1ЃЉИУЪаФабЇЩњЕФЦНОљЩэИпДгЁЁ ЁЁЫъПЊЪМдіМгЬиБ№бИЫйЃЎ
ЃЈ2ЃЉЧѓжБЯпABЫљЖдгІЕФКЏЪ§БэДяЪНЃЎ
ЃЈ3ЃЉжБНгаДГіжБЯпCDЫљЖдгІЕФКЏЪ§БэДяЪНЃЌМйЩш17ЫъКѓИУЪаФаЩњЩэИпдіГЄЫйЖШДѓжТЗћКЯжБЯпCDЫљЖдгІЕФКЏЪ§ЙиЯЕЃЌЧыФудЄВтИУЪа18ЫъФаЩњФъСфзщЕФЦНОљЩэИпДѓдМЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЂй,вбжЊХзЮяЯпy=ax2+bx+cЕФЭМЯёОЙ§ЕуAЃЈ0ЃЌ3)ЁЂBЃЈ1ЃЌ0ЃЉЃЌЦфЖдГЦжсЮЊжБЯпlЃКx=2ЃЌЙ§ЕуAзїACЁЮxжсНЛХзЮяЯпгкЕуCЃЌЁЯAOBЕФЦНЗжЯпНЛЯпЖЮACгкЕуEЃЌЕуPЪЧХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЩшЦфКсзјБъЮЊm.

ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЖЏЕуPдкжБЯпOEЯТЗНЕФХзЮяЯпЩЯЃЌСЌНсPEЁЂPOЃЌЕБmЮЊКЮжЕЪБЃЌЫФБпаЮAOPEУцЛ§зюДѓЃЌВЂЧѓГіЦфзюДѓжЕЃЛ
ЃЈ3ЃЉШчЭМЂкЃЌFЪЧХзЮяЯпЕФЖдГЦжсlЩЯЕФвЛЕуЃЌдкХзЮяЯпЩЯЪЧЗёДцдкЕуPЪЙЁїPOFГЩЮЊвдЕуPЮЊжБНЧЖЅЕуЕФЕШбќжБНЧШ§НЧаЮЃПШєДцдкЃЌжБНгаДГіЫљгаЗћКЯЬѕМўЕФЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌвдACЮЊжБОЖзїЁбOЃЌНЛABгкDЃЌЙ§ЕуOзїOEЁЮABЃЌНЛBCгкEЃЎ
ЃЈ1ЃЉЧѓжЄЃКEDЮЊЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШчЙћЁбOЕФАыОЖЮЊ![]() ЃЌED=2ЃЌбгГЄEOНЛЁбOгкFЃЌСЌНгDFЁЂAFЃЌЧѓЁїADFЕФУцЛ§ЃЎ
ЃЌED=2ЃЌбгГЄEOНЛЁбOгкFЃЌСЌНгDFЁЂAFЃЌЧѓЁїADFЕФУцЛ§ЃЎ

ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮіЃЛЃЈ2ЃЉ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЪзЯШСЌНгODЃЌгЩOEЁЮABЃЌИљОнЦНааЯпгыЕШбќШ§НЧаЮЕФаджЪЃЌвзжЄЕУ![]() Ёе
Ёе![]() МДПЩЕУ
МДПЩЕУ![]() ЃЌдђПЩжЄЕУ
ЃЌдђПЩжЄЕУ![]() ЮЊ
ЮЊ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
ЃЈ2ЃЉСЌНгCDЃЌИљОнжБОЖЫљЖдЕФдВжмНЧЪЧжБНЧЃЌМДПЩЕУ![]() РћгУЙДЙЩЖЈРэМДПЩЧѓЕУ
РћгУЙДЙЩЖЈРэМДПЩЧѓЕУ![]() ЕФГЄЃЌгжгЩOEЁЮABЃЌжЄЕУ
ЕФГЄЃЌгжгЩOEЁЮABЃЌжЄЕУ![]() ИљОнЯрЫЦШ§НЧаЮЕФЖдгІБпГЩБШР§ЃЌМДПЩЧѓЕУ
ИљОнЯрЫЦШ§НЧаЮЕФЖдгІБпГЩБШР§ЃЌМДПЩЧѓЕУ![]() ЕФГЄЃЌШЛКѓРћгУШ§НЧКЏЪ§ЕФжЊЪЖЃЌЧѓЕУ
ЕФГЄЃЌШЛКѓРћгУШ§НЧКЏЪ§ЕФжЊЪЖЃЌЧѓЕУ![]() гы
гы![]() ЕФГЄЃЌШЛКѓРћгУSЁїADF=SЬнаЮABEF-SЬнаЮDBEFЧѓЕУД№АИЃЎ
ЕФГЄЃЌШЛКѓРћгУSЁїADF=SЬнаЮABEF-SЬнаЮDBEFЧѓЕУД№АИЃЎ
ЪдЬтНтЮіЃК(1)жЄУїЃКСЌНгODЃЌ

ЁпOEЁЮABЃЌ
ЁрЁЯCOE=ЁЯCADЃЌЁЯEOD=ЁЯODAЃЌ
ЁпOA=OD,
ЁрЁЯOAD=ЁЯODAЃЌ
ЁрЁЯCOE=ЁЯDOEЃЌ
дкЁїCOEКЭЁїDOEжаЃЌ
 ЁрЁїCOEЁеЁїDOE(SAS)ЃЌ
ЁрЁїCOEЁеЁїDOE(SAS)ЃЌ
![]()
ЁрEDЁЭODЃЌ
ЁрEDЪЧ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
(2)СЌНгCDЃЌНЛOEгкMЃЌ
дкRtЁїODEжаЃЌ
ЁпOD=32ЃЌDE=2ЃЌ
![]()
ЁпOEЁЮABЃЌ
ЁрЁїCOEЁзЁїCABЃЌ
![]() ЁрAB=5ЃЌ
ЁрAB=5ЃЌ
ЁпACЪЧжБОЖЃЌ
![]()
![]()
![]()
![]()
ЁпEFЁЮABЃЌ
![]()
![]()
![]()
ЁрSЁїADF=SЬнаЮABEFSЬнаЮDBEF
![]()
ЁрЁїADFЕФУцЛ§ЮЊ![]()

ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
25
ЁОЬтФПЁПЁОЬтФПЁПвбжЊЃЌХзЮяЯпy=ax2+ax+bЃЈaЁй0ЃЉгыжБЯпy=2x+mгавЛИіЙЋЙВЕуMЃЈ1ЃЌ0ЃЉЃЌЧвaЃМbЃЎ
ЃЈ1ЃЉЧѓbгыaЕФЙиЯЕЪНКЭХзЮяЯпЕФЖЅЕуDзјБъЃЈгУaЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ2ЃЉжБЯпгыХзЮяЯпЕФСэЭтвЛИіНЛЕуМЧЮЊNЃЌЧѓЁїDMNЕФУцЛ§гыaЕФЙиЯЕЪНЃЛ
ЃЈ3ЃЉa=Љ1ЪБЃЌжБЯпy=Љ2xгыХзЮяЯпдкЕкЖўЯѓЯоНЛгкЕуGЃЌЕуGЁЂHЙигкдЕуЖдГЦЃЌЯжНЋЯпЖЮGHбиyжсЯђЩЯЦНвЦtИіЕЅЮЛЃЈtЃО0ЃЉЃЌШєЯпЖЮGHгыХзЮяЯпгаСНИіВЛЭЌЕФЙЋЙВЕуЃЌЪдЧѓtЕФШЁжЕЗЖЮЇЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com