
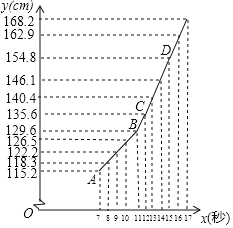
【题目】数学兴趣小组为了研究中小学男生身高y(cm)和年龄x(岁)的关系,从某市官网上得到了该市2017年统计的中小学男生各年龄组的平均身高,见下表:如图已经在直角坐标系中描出了表中数据对应的点,并发现前5个点大致位于直线AB上,后7个点大致位于直线CD上.
年龄组x | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
男生平均身高y | 115.2 | 118.3 | 122.2 | 126.5 | 129.6 | 135.6 | 140.4 | 146.1 | 154.8 | 162.9 | 168.2 |
(1)该市男学生的平均身高从 岁开始增加特别迅速.
(2)求直线AB所对应的函数表达式.
(3)直接写出直线CD所对应的函数表达式,假设17岁后该市男生身高增长速度大致符合直线CD所对应的函数关系,请你预测该市18岁男生年龄组的平均身高大约是多少?
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】在初三综合素质评定结束后,为了了解年级的评定情况,现对初三某班的学生进行了评定等级的调查,绘制了如下男女生等级情况折线统计图和全班等级情况扇形统计图.

(1)调查发现评定等级为合格的男生有2人,女生有1人,则全班共有 名学生.
(2)补全女生等级评定的折线统计图.
(3)根据调查情况,该班班主任从评定等级为合格和A的学生中各选1名学生进行交流,请用树形图或表格求出刚好选中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,并填空:
我们学过的一些代数公式很多都可以通过表示几何图形面积的方法进行直观推导和解释。例如:平方差公式、完全平方公式。
(提出问题)如何用表示几何图形面积的方法推证:![]()
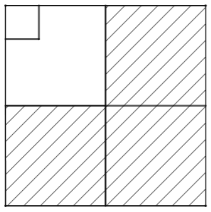
(规律探索)观察下面表示几何图形面积的方法:

分可以看成3个![]() 的正方形,总面积
的正方形,总面积![]() ,得到
,得到![]()
(解决问题)归纳猜想(不需要证明)
![]() (用含n的代数式表示)
(用含n的代数式表示)
(拓展应用)根据以上结论,计算:![]() ,直接写答案
,直接写答案
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】幸福村在推进美丽乡村建设中,决定建设幸福广场,计划铺设相同大小、规格的红色和蓝色地砖,经过调查,获取信息如下表:
类别 | 购买数量低于500块 | 购买数量不低于500块 |
红色地砖 | 原价销售 | 以八折销售 |
蓝色地砖 | 原价销售 | 以九折销售 |
若购买红色地砖400块,蓝色地砖600块,需付款8600元;若购买红色地砖1000块,蓝色地砖350块,需付款9900元.
(1)红色地砖和蓝色地砖的单价各多少元?
(2)经过测算,需要购置地砖1200块,其中蓝色地砖的数量不少于红色地砖的一半,并且不超过600块,如何购买付款最少?最少是多少元?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个运输小队分别从两个仓库以相同的工作效率调运一批物资,两队同时开始工作.第二小队工作5天后,由于技术问题检修设备5天,为赶上进度,再次开工后他们将工作效率提高到原先的2倍,结果和第一小队同时完成任务.在两队调运物资的过程中,两个仓库物资的剩余量y t与第一小队工作时间x天的函数图像如图所示.

(1)①求线段AC所表示的y与x之间的函数表达式;
②求点F的坐标,并解释点F的实际意义.
(2)如果第二小队没有检修设备,按原来的工作效率正常工作,那么他们完成任务的天数是 天.
查看答案和解析>>
科目:初中数学 来源: 题型:
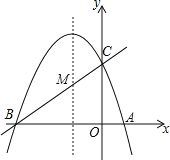
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:

(1)在这次调查中,喜欢篮球项目的同学有 人,在扇形统计图中,“乒乓球”的百分比为 %,如果学校有800名学生,估计全校学生中有 人喜欢篮球项目.
(2)请将条形统计图补充完整.
(3)在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学.现要从中随机抽取2名同学代表班级参加校篮球队,请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
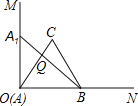
【题目】已知∠MON=90°,等边三角形ABC的一个顶点B是射线ON上的一定点,顶点A于点O重合,顶点C在∠MON内部
(1)当点A在射线OM上移动到A1时,连接A1B,请在∠MON内部作出以A1B为一边的等边三角形A1BC1(保留作图痕迹,不写作法);
(2)设A1B与OC交于点Q,BC的延长线与A1C1交于点D.求证:△BCQ∽△BA1D;
(3)连接CC1,试猜想∠BCC1为多少度,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
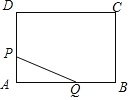
【题目】如图,矩形ABCD中,AB=8cm,BC=6cm,点P从点A出发,以lcm/s的速度沿A→D→C方向匀速运动,同时点Q从点A出发,以2cm/s的速度沿A→B→C方向匀速运动,当一个点到达点C时,另一个点也随之停止.设运动时间为t(s),△APQ的面积为S(cm2),下列能大致反映S与t之间函数关系的图象是( )
A. 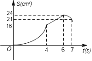 B.
B. 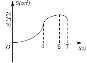 C.
C. 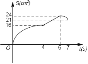 D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com