
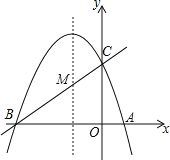
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ≈ΉΈοœΏyΘΫax2+bx+c(aΓΌ0)ΒΡΕ‘≥Τ÷αΈΣ÷±œΏxΘΫ©¹1Θ§«“≈ΉΈοœΏΨ≠ΙΐA(1Θ§0)Θ§C(0Θ§3)ΝΫΒψΘ§”κx÷αΫΜ”ΎΒψBΘ°
(1)»τ÷±œΏyΘΫmx+nΨ≠ΙΐBΓΔCΝΫΒψΘ§«σ÷±œΏBCΚΆ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
(2)‘Ύ≈ΉΈοœΏΒΡΕ‘≥Τ÷αxΘΫ©¹1…œ’““ΜΒψMΘ§ ΙΒψMΒΫΒψAΒΡΨύάκ”κΒΫΒψCΒΡΨύάκ÷°ΚΆΉν–ΓΘ§«σ≥ωΒψMΒΡΉχ±ξΘΜ
(3)…ηΒψPΈΣ≈ΉΈοœΏΒΡΕ‘≥Τ÷αxΘΫ©¹1…œΒΡ“ΜΗωΕ·ΒψΘ§«σ ΙΓςBPCΈΣ÷±Ϋ«»ΐΫ«–ΈΒΡΒψPΒΡΉχ±ξΘ°
ΓΨ¥πΑΗΓΩ(1)≈ΉΈοœΏΫβΈω ΫΈΣyΘΫ©¹x2©¹2x+3Θ§÷±œΏΒΡΫβΈω ΫΈΣyΘΫx+3ΘΜ(2)Β±ΒψMΒΫΒψAΒΡΨύάκ”κΒΫΒψCΒΡΨύάκ÷°ΚΆΉν–Γ ±MΒΡΉχ±ξΈΣ(©¹1Θ§2)ΘΜ(3)PΒΡΉχ±ξΈΣ(©¹1Θ§©¹2)Μρ(©¹1Θ§4)Μρ(©¹1Θ§![]() ) Μρ(©¹1Θ§
) Μρ(©¹1Θ§![]() )Θ°
)Θ°
ΓΨΫβΈωΓΩ
![]() œ»Α―ΒψAΘ§CΒΡΉχ±ξΖ÷±π¥ζ»κ≈ΉΈοœΏΫβΈω ΫΒΟΒΫaΚΆbΘ§cΒΡΙΊœΒ ΫΘ§‘ΌΗυΨί≈ΉΈοœΏΒΡΕ‘≥Τ÷αΖΫ≥ΧΩ…ΒΟaΚΆbΒΡΙΊœΒΘ§‘ΌΝΣΝΔΒΟΒΫΖΫ≥ΧΉιΘ§ΫβΖΫ≥ΧΉιΘ§«σ≥ωaΘ§bΘ§cΒΡ÷ΒΦ¥Ω…ΒΟΒΫ≈ΉΈοœΏΫβΈω ΫΘΜΑ―BΓΔCΝΫΒψΒΡΉχ±ξ¥ζ»κ÷±œΏ
œ»Α―ΒψAΘ§CΒΡΉχ±ξΖ÷±π¥ζ»κ≈ΉΈοœΏΫβΈω ΫΒΟΒΫaΚΆbΘ§cΒΡΙΊœΒ ΫΘ§‘ΌΗυΨί≈ΉΈοœΏΒΡΕ‘≥Τ÷αΖΫ≥ΧΩ…ΒΟaΚΆbΒΡΙΊœΒΘ§‘ΌΝΣΝΔΒΟΒΫΖΫ≥ΧΉιΘ§ΫβΖΫ≥ΧΉιΘ§«σ≥ωaΘ§bΘ§cΒΡ÷ΒΦ¥Ω…ΒΟΒΫ≈ΉΈοœΏΫβΈω ΫΘΜΑ―BΓΔCΝΫΒψΒΡΉχ±ξ¥ζ»κ÷±œΏ![]() Θ§ΫβΖΫ≥ΧΉι«σ≥ωmΚΆnΒΡ÷ΒΦ¥Ω…ΒΟΒΫ÷±œΏΫβΈω ΫΘΜ
Θ§ΫβΖΫ≥ΧΉι«σ≥ωmΚΆnΒΡ÷ΒΦ¥Ω…ΒΟΒΫ÷±œΏΫβΈω ΫΘΜ
![]() …η÷±œΏBC”κΕ‘≥Τ÷α
…η÷±œΏBC”κΕ‘≥Τ÷α![]() ΒΡΫΜΒψΈΣMΘ§‘ρ¥Υ ±
ΒΡΫΜΒψΈΣMΘ§‘ρ¥Υ ±![]() ΒΡ÷ΒΉν–Γ
ΒΡ÷ΒΉν–Γ![]() Α―
Α―![]() ¥ζ»κ÷±œΏ
¥ζ»κ÷±œΏ![]() ΒΟyΒΡ÷ΒΘ§Φ¥Ω…«σ≥ωΒψMΉχ±ξΘΜ
ΒΟyΒΡ÷ΒΘ§Φ¥Ω…«σ≥ωΒψMΉχ±ξΘΜ
![]() …η
…η![]() Θ§”÷“ρΈΣ
Θ§”÷“ρΈΣ![]() Θ§
Θ§![]() Θ§Υυ“‘Ω…ΒΟ
Θ§Υυ“‘Ω…ΒΟ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§‘ΌΖ÷»ΐ÷÷«ιΩωΖ÷±πΧ÷¬έ«σ≥ωΖϊΚœΧβ“βt÷ΒΦ¥Ω…«σ≥ωΒψPΒΡΉχ±ξΘ°
Θ§‘ΌΖ÷»ΐ÷÷«ιΩωΖ÷±πΧ÷¬έ«σ≥ωΖϊΚœΧβ“βt÷ΒΦ¥Ω…«σ≥ωΒψPΒΡΉχ±ξΘ°
ΫβΘΚ(1)“άΧβ“βΒΟΘΚ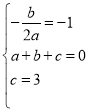 Θ§
Θ§
Ϋβ÷°ΒΟΘΚ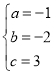 Θ§
Θ§
Γύ≈ΉΈοœΏΫβΈω ΫΈΣyΘΫ©¹x2©¹2x+3
ΓΏΕ‘≥Τ÷αΈΣxΘΫ©¹1Θ§«“≈ΉΈοœΏΨ≠ΙΐA(1Θ§0)Θ§
ΓύΑ―B(©¹3Θ§0)ΓΔC(0Θ§3)Ζ÷±π¥ζ»κ÷±œΏyΘΫmx+nΘ§
ΒΟ![]() Θ§
Θ§
Ϋβ÷°ΒΟΘΚ![]() Θ§
Θ§
Γύ÷±œΏyΘΫmx+nΒΡΫβΈω ΫΈΣyΘΫx+3ΘΜ
(2)…η÷±œΏBC”κΕ‘≥Τ÷αxΘΫ©¹1ΒΡΫΜΒψΈΣMΘ§‘ρ¥Υ ±MA+MCΒΡ÷ΒΉν–ΓΘ°
Α―xΘΫ©¹1¥ζ»κ÷±œΏyΘΫx+3ΒΟΘ§yΘΫ2Θ§
ΓύM(©¹1Θ§2)Θ§
Φ¥Β±ΒψMΒΫΒψAΒΡΨύάκ”κΒΫΒψCΒΡΨύάκ÷°ΚΆΉν–Γ ±MΒΡΉχ±ξΈΣ(©¹1Θ§2)ΘΜ
(3)…ηP(©¹1Θ§t)Θ§
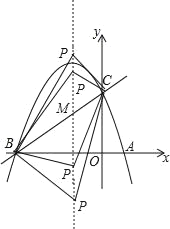
”÷ΓΏB(©¹3Θ§0)Θ§C(0Θ§3)Θ§
ΓύBC2ΘΫ18Θ§PB2ΘΫ(©¹1+3)2+t2ΘΫ4+t2Θ§PC2ΘΫ(©¹1)2+(t©¹3)2ΘΫt2©¹6t+10Θ§
ΔΌ»τΒψBΈΣ÷±Ϋ«ΕΞΒψΘ§‘ρBC2+PB2ΘΫPC2Φ¥ΘΚ18+4+t2ΘΫt2©¹6t+10Ϋβ÷°ΒΟΘΚtΘΫ©¹2ΘΜ
ΔΎ»τΒψCΈΣ÷±Ϋ«ΕΞΒψΘ§‘ρBC2+PC2ΘΫPB2Φ¥ΘΚ18+t2©¹6t+10ΘΫ4+t2Ϋβ÷°ΒΟΘΚtΘΫ4Θ§
Δέ»τΒψPΈΣ÷±Ϋ«ΕΞΒψΘ§‘ρPB2+PC2ΘΫBC2Φ¥ΘΚ4+t2+t2©¹6t+10ΘΫ18Ϋβ÷°ΒΟΘΚt1ΘΫ![]() Θ§t2ΘΫ
Θ§t2ΘΫ![]() ΘΜ
ΘΜ
Ήέ…œΥυ ωPΒΡΉχ±ξΈΣ(©¹1Θ§©¹2)Μρ(©¹1Θ§4)Μρ(©¹1Θ§![]() ) Μρ(©¹1Θ§
) Μρ(©¹1Θ§![]() )Θ°
)Θ°


 »Ϊ”≈ΒψΝΖΒΞ‘ΣΦΤΜ°œΒΝ–¥πΑΗ
»Ϊ”≈ΒψΝΖΒΞ‘ΣΦΤΜ°œΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
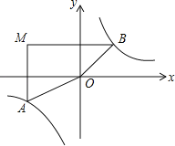
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΙΐΒψMΘ®©¹5Θ§3Θ©Ζ÷±πΉςx÷αΘ§y÷αΒΡ¥ΙœΏ”κΖ¥±»άΐΚ· ΐyΘΫ![]() ΒΡΆΦœσΫΜ”ΎAΘ§BΝΫΒψΘ§»τΥΡ±Ώ–ΈMAOBΒΡΟφΜΐΈΣ24Θ§‘ρkΘΫ_____Θ°
ΒΡΆΦœσΫΜ”ΎAΘ§BΝΫΒψΘ§»τΥΡ±Ώ–ΈMAOBΒΡΟφΜΐΈΣ24Θ§‘ρkΘΫ_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΓΑ ΐ―ßά¥‘¥”Ύ…ζΜνΘ§”÷‘Υ”Ο”Ύ…ζΜνΓ±≤ήάœ ΠΈΣΝΥΝΥΫβΥυΫΧΑύΦΕ―ß…ζάϊ”Ο ΐ―ß÷Σ ΕΫβΨω ΒΦ Έ ΧβΒΡΡήΝΠΘ§±ύ÷Τ»τΗ…Έ ΧβΕ‘»ΪΑύ―ß…ζΫχ––ΝΥ“Μ¥Έ≤β ‘Θ§≤ΔΫΪ≤β ‘ΫαΙϊΖ÷≥…ΥΡάύΘ§AΧΊ±π«ΩΘΚBΘΚ«ΩΘΜCΘΚ“ΜΑψΘΚDΫœ»θ“‘œ¬ «”…Βς≤ι≤β ‘ΫαΙϊΜφ÷ΤΒΡΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘ§«κΡψΗυΨίΆ≥ΦΤΆΦΆξ≥…“‘œ¬Ϋβ¥πΘ°
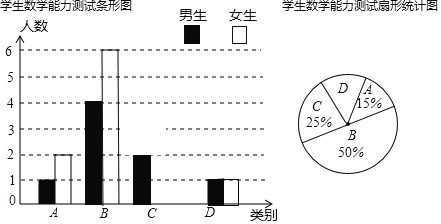
Θ®1Θ©≤ήάœ ΠΒΡΑύΦΕΙ≤”–ΓΓ ΓΓΟϊ―ß…ζΘΜ
Θ®2Θ©ΫΪœ¬ΟφΧθ–ΈΆ≥ΦΤΆΦΒΡCάύ≤ΩΖ÷≤Ι≥δΆξ’ϊΘΜ
Θ®3Θ©…»–ΈΆ≥ΦΤΆΦ÷–Θ§DάύΕ‘”ΠΒΡ‘≤–ΡΫ«ΈΣΕύ…ΌΕ»Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ“Μ÷Μ≤ΜΆΗΟςΒΡ¥ϋΉ”÷–ΉΑ”–1ΗωΚλ…Ϊ–Γ«ρΘ§2ΗωΜΤ…Ϊ–Γ«ρΚΆ»τΗ…ΗωΚΎ…Ϊ–Γ«ρΘ§’β–©–Γ«ρ≥ΐ―’…Ϊ“‘ΆβΕΦ“Μ―υΘ°“―÷Σ¥”¥ϋ÷–»Έ“βΟΰ≥ω1ΗωΚλ…Ϊ–Γ«ρΒΡΗ≈¬ «![]() Θ°
Θ°
Θ®1Θ©¥ϋ÷–ΚΎ…Ϊ–Γ«ρΒΡ ΐΝΩ « ΗωΘΜ
Θ®2Θ©»τ¥”¥ϋ÷–ΥφΜζΟΰ≥ω1Ηω–Γ«ρΘ§Φ«¬ΦΚΟ―’…ΪΚσΖ≈ΜΊ¥ϋ÷–≤ΔΫΝ‘»Θ§‘Ό¥”¥ϋ÷–»Έ“βΟΰ≥ω1Ηω–Γ«ρΘ§«σΝΫ¥ΈΟΰ≥ωΒΡΕΦ «ΜΤ…Ϊ–Γ«ρΒΡΗ≈¬ «Εύ…ΌΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
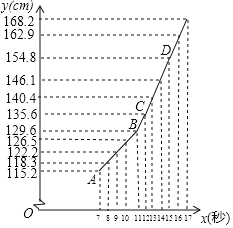
ΓΨΧβΡΩΓΩ ΐ―ß–Υ»Λ–ΓΉιΈΣΝΥ―–ΨΩ÷––Γ―ßΡ–…ζ…μΗΏyΘ®cmΘ©ΚΆΡξΝδxΘ®ΥξΘ©ΒΡΙΊœΒΘ§¥”Ρ≥ –ΙΌΆχ…œΒΟΒΫΝΥΗΟ –2017ΡξΆ≥ΦΤΒΡ÷––Γ―ßΡ–…ζΗςΡξΝδΉιΒΡΤΫΨυ…μΗΏΘ§Φϊœ¬±μΘΚ»γΆΦ“―Ψ≠‘Ύ÷±Ϋ«Ήχ±ξœΒ÷–Οη≥ωΝΥ±μ÷– ΐΨίΕ‘”ΠΒΡΒψΘ§≤ΔΖΔœ÷«Α5ΗωΒψ¥σ÷¬ΈΜ”Ύ÷±œΏAB…œΘ§Κσ7ΗωΒψ¥σ÷¬ΈΜ”Ύ÷±œΏCD…œΘ°
ΡξΝδΉιx | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
Ρ–…ζΤΫΨυ…μΗΏy | 115.2 | 118.3 | 122.2 | 126.5 | 129.6 | 135.6 | 140.4 | 146.1 | 154.8 | 162.9 | 168.2 |
Θ®1Θ©ΗΟ –Ρ–―ß…ζΒΡΤΫΨυ…μΗΏ¥”ΓΓ ΓΓΥξΩΣ Φ‘ωΦ”ΧΊ±π―ΗΥΌΘ°
Θ®2Θ©«σ÷±œΏABΥυΕ‘”ΠΒΡΚ· ΐ±μ¥ο ΫΘ°
Θ®3Θ©÷±Ϋ”–¥≥ω÷±œΏCDΥυΕ‘”ΠΒΡΚ· ΐ±μ¥ο ΫΘ§ΦΌ…η17ΥξΚσΗΟ –Ρ–…ζ…μΗΏ‘ω≥ΛΥΌΕ»¥σ÷¬ΖϊΚœ÷±œΏCDΥυΕ‘”ΠΒΡΚ· ΐΙΊœΒΘ§«κΡψ‘Λ≤βΗΟ –18ΥξΡ–…ζΡξΝδΉιΒΡΤΫΨυ…μΗΏ¥σ‘Φ «Εύ…ΌΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΨΊ–Έ÷ΫΤ§ABCDΘ§AD=4Θ§AB=3Θ§»γΙϊΒψE‘Ύ±ΏBC…œΘ§ΫΪ÷ΫΤ§―ΊAE’έΒΰΘ§ ΙΒψB¬δ‘ΎΒψF¥ΠΘ§ΝΣΫαFCΘ§Β±ΓςEFC «÷±Ϋ«»ΐΫ«–Έ ±Θ§Ρ«Ο¥BEΒΡ≥ΛΈΣ____________Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΔΌ,“―÷Σ≈ΉΈοœΏy=ax2+bx+cΒΡΆΦœώΨ≠ΙΐΒψAΘ®0Θ§3)ΓΔBΘ®1Θ§0Θ©Θ§ΤδΕ‘≥Τ÷αΈΣ÷±œΏlΘΚx=2Θ§ΙΐΒψAΉςACΓΈx÷αΫΜ≈ΉΈοœΏ”ΎΒψCΘ§ΓœAOBΒΡΤΫΖ÷œΏΫΜœΏΕΈAC”ΎΒψEΘ§ΒψP «≈ΉΈοœΏ…œΒΡ“ΜΗωΕ·ΒψΘ§…ηΤδΚαΉχ±ξΈΣm.

Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©»τΕ·ΒψP‘Ύ÷±œΏOEœ¬ΖΫΒΡ≈ΉΈοœΏ…œΘ§Ν§ΫαPEΓΔPOΘ§Β±mΈΣΚΈ÷Β ±Θ§ΥΡ±Ώ–ΈAOPEΟφΜΐΉν¥σΘ§≤Δ«σ≥ωΤδΉν¥σ÷ΒΘΜ
Θ®3Θ©»γΆΦΔΎΘ§F «≈ΉΈοœΏΒΡΕ‘≥Τ÷αl…œΒΡ“ΜΒψΘ§‘Ύ≈ΉΈοœΏ…œ «Ζώ¥φ‘ΎΒψP ΙΓςPOF≥…ΈΣ“‘ΒψPΈΣ÷±Ϋ«ΕΞΒψΒΡΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§÷±Ϋ”–¥≥ωΥυ”–ΖϊΚœΧθΦΰΒΡΒψPΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§÷±œΏy1ΘΫ2x+2ΫΜx÷αΓΔy÷α”ΎΒψAΓΔCΘ§÷±œΏ![]() ΫΜx÷αΓΔy÷α”ΎΒψBΓΔCΘ§ΒψP(mΘ§1) «ΓςABCΡΎ≤Ω(Αϋά®±Ώ…œ)ΒΡ“ΜΒψΘ§‘ρmΒΡΉν¥σ÷Β”κΉν–Γ÷Β÷°≤νΈΣ(ΓΓΓΓ)
ΫΜx÷αΓΔy÷α”ΎΒψBΓΔCΘ§ΒψP(mΘ§1) «ΓςABCΡΎ≤Ω(Αϋά®±Ώ…œ)ΒΡ“ΜΒψΘ§‘ρmΒΡΉν¥σ÷Β”κΉν–Γ÷Β÷°≤νΈΣ(ΓΓΓΓ)
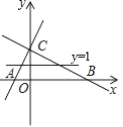
A.2B.2.5C.3D.3.5
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ”–’β―υ“ΜΗωΈ ΧβΘΚΧΫΨΩΚ· ΐ![]() ΒΡΆΦœσ”κ–‘÷ .–ΓΆ°ΗυΨί―ßœΑΚ· ΐΒΡΨ≠―ιΘ§Ε‘Κ· ΐ
ΒΡΆΦœσ”κ–‘÷ .–ΓΆ°ΗυΨί―ßœΑΚ· ΐΒΡΨ≠―ιΘ§Ε‘Κ· ΐ![]() ΒΡΆΦœσ”κ–‘÷ Ϋχ––ΝΥΧΫΨΩ.œ¬Οφ «–ΓΆ°ΧΫΨΩΒΡΙΐ≥ΧΘ§«κ≤Ι≥δΆξ’ϊΘΚ
ΒΡΆΦœσ”κ–‘÷ Ϋχ––ΝΥΧΫΨΩ.œ¬Οφ «–ΓΆ°ΧΫΨΩΒΡΙΐ≥ΧΘ§«κ≤Ι≥δΆξ’ϊΘΚ
x | -4 | -3.5 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 3.5 | 4 | ||
y |
|
|
|
|
| 0 |
|
| m |
|
|
Θ®1Θ©«σmΒΡ÷ΒΈΣ ΘΜ
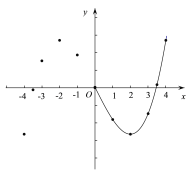
Θ®2Θ©»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒx0y ÷–Θ§Οη≥ωΝΥ“‘…œ±μ÷–ΗςΕ‘Ε‘”Π÷ΒΈΣΉχ±ξΒΡΒψΘ§ΗυΨίΟη≥ωΒΡΒψΘ§Μ≠≥ωΝΥΆΦœσΒΡ“Μ≤ΩΖ÷Θ§«κΗυΨί Θ”ύΒΡΒψ≤Ι»Ϊ¥ΥΚ· ΐΒΡΆΦœσΘΜ
Θ®3Θ©ΖΫ≥Χ![]() Β ΐΗυΒΡΗω ΐΈΣ ΘΜ
Β ΐΗυΒΡΗω ΐΈΣ ΘΜ
Θ®4Θ©Ιέ≤λΆΦœσΘ§–¥≥ωΗΟΚ· ΐΒΡ“ΜΧθ–‘÷ ΘΜ
Θ®5Θ©‘ΎΒΎΘ®2Θ©Έ ΒΡΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Μ≠≥ω÷±œΏ![]() Θ§ΗυΨίΆΦœσ–¥≥ωΖΫ≥Χ
Θ§ΗυΨίΆΦœσ–¥≥ωΖΫ≥Χ![]() ΒΡ“ΜΗω’ΐ ΐΗυ‘ΦΈΣ Θ®ΨΪ»ΖΒΫ0.1Θ©.
ΒΡ“ΜΗω’ΐ ΐΗυ‘ΦΈΣ Θ®ΨΪ»ΖΒΫ0.1Θ©.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com