【题目】已知A－B=7a2－7ab，且B=－4a2＋5ab＋8．（1）求A等于多少？
（2）若
，求A的值．
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目：初中数学 来源： 题型：
【题目】2018无锡市体育中考男生项目分为速度耐力类、力量类和灵巧类，每位考生只能在三类中各选一项进行考试．其中速度耐力类项目有：50米跑、800米跑、50米游泳；力量类项目有：掷实心球、引体向上；灵巧类项目有：30秒钟跳绳、立定跳远、俯卧撑、篮球运球．男生小明“50米跑”是强项，他决定必选，其它项目在平时测试中成绩完全相同，他决定随机选择．
（1）请用画树状图或列表的方法求“小明‘选50米跑、引体向上和立定跳远’”的概率；
（2）小明所选的项目中有立定跳远的概率是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）发现：
如图1，点A为线段BC外一动点，且BC=a，AB=b．
填空：当点A位于 时，线段AC的长取得最大值，且最大值为 （用含a，b的式子表示）
（2）应用：
点A为线段BC外一动点，且BC=3，AB=1，如图2所示，分别以AB，AC为边，作等边三角形ABD和等边三角形ACE，连接CD，BE．
①请找出图中与BE相等的线段，并说明理由；
②直接写出线段BE长的最大值．
（3）拓展：
如图3，在平面直角坐标系中，点A的坐标为（2，0），点B的坐标为（5，0），点P为线段AB外一动点，且PA=2，PM=PB，∠BPM=90°，请直接写出线段AM长的最大值及此时点P的坐标．
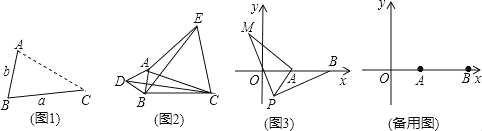
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了美化环境，建设宜居成都，我市准备在一个广场上种植甲、乙两种花卉.经市场调查，甲种花卉的种植费用
（元）与种植面积
之间的函数关系如图所示，乙种花卉的种植费用为每平方米100元.
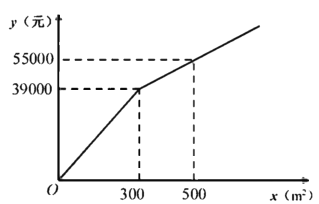
（1）直接写出当
和
时，与
的函数关系式；
（2）广场上甲、乙两种花卉的种植面积共
，若甲种花卉的种植面积不少于
，且不超过乙种花卉种植面积的2倍，那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少？最少总费用为多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】赵老师是一名健步走运动的爱好者为备战2019中国地马拉松系列赛·广元站10千米群众健身赛，她用手机软件记录了某个月（30天）每天健步走的步数（单位：万步），将记录结果绘制成了如图所示的统计图在每天健步走的步数这组数据中，众数和中位数分别是（ ）
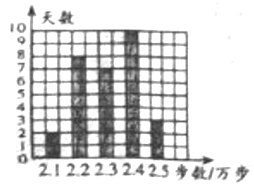
A. 2.2，2.3B. 2.4，2.3C. 2.4,2.35D. 2.3，2.3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下表是某校“河南省汉子听写大赛初赛”冠军组成员的年龄分布
年龄/岁 | 12 | 13 | 14 | 15 |
人数 | 5 | 15 | x | 12﹣x |
对于不同的x，下列关于年龄的统计量不会发生改变的是（ ）
A. 平均数、中位数 B. 平均数、方差 C. 众数、中位数 D. 中位数、方差
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义运算a
b＝a(1－b)，下面给出了关于这种运算的四个结论：
①2(－2)＝6 ②ab＝ba
③若a＋b＝0，则(aa)＋(bb)＝2ab ④若ab＝0，则a＝0．
其中正确结论的序号是 (填上你认为所有正确结论的序号)．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】请将下列证明过程补充完整：
已知：如图，点B、E分别在AC、DF上，AF分别交BD、CE于点M、N，∠1=∠2，∠A=∠F．求证：∠C=∠D．
证明：∵∠1=∠2（已知），
又∵∠1=∠ANC（ ），
∴ ∠=∠（等量代换）．
∴ ∥ （ ），
∴∠ABD=∠C（ ）．
又∵∠A=∠F（已知），
∴ ∥ （ ）．
∴ ∠=∠ （ ）．
∴∠C=∠D（ ）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
