
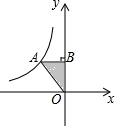
 如图,已知A点是反比例函数y=$\frac{k}{x}$(x<0)图象上一点,AB⊥y轴于B,且△AOB的面积为3,则k的值为-6.
如图,已知A点是反比例函数y=$\frac{k}{x}$(x<0)图象上一点,AB⊥y轴于B,且△AOB的面积为3,则k的值为-6. 分析 根据反比例函数y=$\frac{k}{x}$(k≠0)系数k的几何意义得到S△ABO=$\frac{1}{2}$|k|=3,解得k=6或-6,然后根据反比例函数的性质得到满足条件的k的值.
解答 解:∵S△ABO=$\frac{1}{2}$|k|,△AOB的面积是3,
∴$\frac{1}{2}$|k|=3,
解得k=6或-6,
∵反比例函数图象分布在第二、四象限,
∴k<0,
∴k=-6.
故答案为:-6.
点评 本题考查了反比例函数y=$\frac{k}{x}$(k≠0)系数k的几何意义:从反比例函数y=$\frac{k}{x}$(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.


 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | C. | $\sqrt{{5}^{2}-{3}^{2}}$=5-3 | D. | $\sqrt{8}$$÷\sqrt{2}$=4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 没有水分,种子发芽 | B. | 小张买了一张彩票中500万大奖 | ||
| C. | 抛一枚骰子,正面向上的点数是7 | D. | 367人中至少有2人的生日相同 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com