
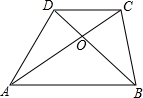
 如图,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O,有下面四个结论:①△AOB∽△COD;②△AOD∽△BOC;③S△AOD=S△BOC;④S△DOC:S△BOA=DC:AB,其中,结论一定正确的有( )
如图,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O,有下面四个结论:①△AOB∽△COD;②△AOD∽△BOC;③S△AOD=S△BOC;④S△DOC:S△BOA=DC:AB,其中,结论一定正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据相似三角形的判定定理即可得到△AOB∽△COD,故①正确;根据相似三角形的性质即可得到S△COD:S△BOA=($\frac{DC}{AB}$)2,故④错误;设梯形ABCD的高为h,则S△ABD=$\frac{1}{2}$•AB•h,S△ABC=$\frac{1}{2}$•AB•h,于是得到S△ABC=S△ABD,推出S△AOD=S△BOC,故③正确;在△AOD与△BOC中,只有∠AOD=∠BOC,再找不到任何一对角相等,也不能说明夹此角的两边对应成比例,故②错误.
解答 解:∵AB∥CD,
∴∠OAB=∠OCD,∠OBA=∠ODC,
∴△AOB∽△COD,故①正确;
∴S△COD:S△BOA=($\frac{DC}{AB}$)2,故④正确;
设梯形ABCD的高为h,则S△ABD=$\frac{1}{2}$•AB•h,S△ABC=$\frac{1}{2}$•AB•h,
∴S△ABC=S△ABD,
∴S△AOD=S△BOC,故③正确;
在△AOD与△BOC中,只有∠AOD=∠BOC,再找不到任何一对角相等,也不能说明夹此角的两边对应成比例,故②错误.
故结论始终正确的序号是①③,共2个.
故选B.
点评 此题综合考查了相似三角形的判定及性质、求三角形的面积比的方法:面积公式,相似三角形的性质,熟练掌握相似三角形的判定和性质是解题的关键.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:填空题
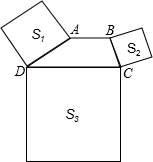 如图,在梯形ABCD中,AB∥DC,∠ADC+∠BCD=90°,且DC=2AB,分别以DA、BC、DC为边向梯形外作正方形,其面积分别为S1=7,S2=4,则S3的面积是44.
如图,在梯形ABCD中,AB∥DC,∠ADC+∠BCD=90°,且DC=2AB,分别以DA、BC、DC为边向梯形外作正方形,其面积分别为S1=7,S2=4,则S3的面积是44.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
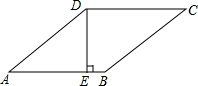 如图,在菱形ABCD中,DE⊥AB,垂足为E,DE=4,sinA=$\frac{2}{5}$,则菱形ABCD的周长是( )
如图,在菱形ABCD中,DE⊥AB,垂足为E,DE=4,sinA=$\frac{2}{5}$,则菱形ABCD的周长是( )| A. | 10 | B. | 20 | C. | 30 | D. | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
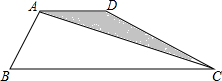 如图,四边形ABCD中,AB=AD,AD∥BC,∠ABC=60°,∠BCD=30°,BC=6,那么△ACD的面积是$\sqrt{3}$.
如图,四边形ABCD中,AB=AD,AD∥BC,∠ABC=60°,∠BCD=30°,BC=6,那么△ACD的面积是$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com