Question

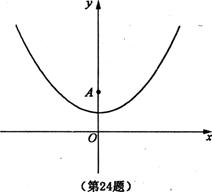
已知抛物线y=x² + 1(如图所示)．

    (1)填空：抛物线的顶点坐标是(______，______)，对称轴是_____；

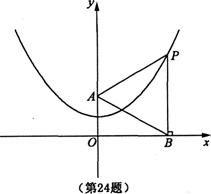
    (2)已知y轴上一点A(0，2)，点P在抛物线上，过点P作PB⊥x轴，垂足为B．若△PAB是等边三角形，求点P的坐标；

 (3)在(2)的条件下，点M在直线AP上．在平面内是否存在点N，使四边形OAMN为菱形?若存在，直接写出所有满足条件的点N的坐标；若不存在，请说明理由．

Answer 1

    解：(1)顶点坐标是(0，1)，对称轴是y轴(或x=O)．

         ……………………………………………4分

       (2) ∵△PAB是等边三角形，   

           ∴∠ABO=90^o-60^o=30^o．

           ∴AB=20A=4．∴PB=4．………………5分

解法一：把y=4代人y=x² + 1，

得  x=±2.   

       ∴P₁(2，4)，P₂(-2，4)． 

       解法二：∴OB==2    

       ∴P₁(2，4)．    …………………………………………………………………7分

       根据抛物线的对称性，得P₂(-2，4)．  ………………………………………8分

       (3)存在.N₁(，1)，N₂(-，-1)，N₃(-，1)，N₄(，-1). …………12分