
【题目】(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下列两题:
①如图3,在四边形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=12,E是AB上一点,且∠DCE=45°,BE=4,则DE= .
②如图4,在△ABC中,∠BAC=45°,AD⊥BC,且BD=2,AD=6,求△ABC的面积.
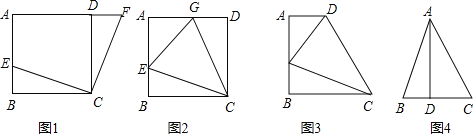
【答案】(1)见解析;(2)见解析;(3)①DE=10;②△ABC的面积是15.
【解析】
(1)根据正方形的性质,可直接证明△CBE≌△CDF,从而得出CE=CF;
(2)延长AD至F,使DF=BE,连接CF,根据(1)知∠BCE=∠DCF,即可证明∠ECF=∠BCD=90°,根据∠GCE=45°,得∠GCF=∠GCE=45°,利用全等三角形的判定方法得出△ECG≌△FCG,即GE=GF,即可得出答案GE=DF+GD=BE+GD;
(3)①过C作CF⊥AD的延长线于点F.则四边形ABCF是正方形,设DF=x,则AD=12-x,根据(2)可得:DE=BE+DF=4+x,在直角△ADE中利用勾股定理即可求解;
②作∠EAB=∠BAD,∠GAC=∠DAC,过B作AE的垂线,垂足是E,过C作AG的垂线,垂足是G,BE和GC相交于点F,BF=6-2=4,设GC=x,则CD=GC=x,FC=6-x,BC=2+x.在直角△BCF中利用勾股定理求得CD的长,则三角形的面积即可求解.
(1)证明:如图1,在正方形ABCD中,
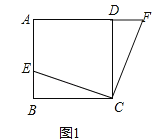
∵BC=CD,∠B=∠CDF,BE=DF,
∴△CBE≌△CDF,
∴CE=CF;
(2)证明:如图2,延长AD至F,使DF=BE,连接CF,
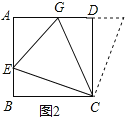
由(1)知△CBE≌△CDF,
∴∠BCE=∠DCF.
∴∠BCE+∠ECD=∠DCF+∠ECD
即∠ECF=∠BCD=90°,
又∵∠GCE=45°,∴∠GCF=∠GCE=45°,
∵CE=CF,∠GCE=∠GCF,GC=GC,
∴△ECG≌△FCG,
∴GE=GF,
∴GE=DF+GD=BE+GD;
(3)①过C作CF⊥AD的延长线于点F.则四边形ABCF是正方形.
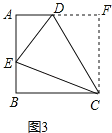
AE=AB﹣BE=12﹣4=8,
设DF=x,则AD=12﹣x,
根据(2)可得:DE=BE+DF=4+x,
在直角△ADE中,AE2+AD2=DE2,则82+(12﹣x)2=(4+x)2,
解得:x=6.
则DE=4+6=10.
故答案是:10;
②作∠EAB=∠BAD,∠GAC=∠DAC,过B作AE的垂线,垂足是E,过C作AG的垂线,垂足是G,BE和GC相交于点F,则四边形AEFG是正方形,且边长=AD=6,BE=BD=2,
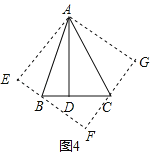
则BF=6﹣2=4,设GC=x,则CD=GC=x,FC=6﹣x,BC=2+x.
在直角△BCF中,BC2=BF2+FC2,
则(2+x)2=42+x2,
解得:x=3.
则BC=2+3=5,
则△ABC的面积是:![]() ADBC=
ADBC=![]() ×6×5=15.
×6×5=15.


科目:初中数学 来源: 题型:
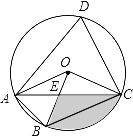
【题目】如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,∠AOB=![]() ∠COB,⊙O的半径为
∠COB,⊙O的半径为![]() ,连接AC交OB于点E,OB与AC相交于点E,则图中阴影部分面积是( )
,连接AC交OB于点E,OB与AC相交于点E,则图中阴影部分面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校有n名师生乘坐m辆客车外出参观,若每辆客车坐45人,则还有28人没有上车;若每辆客车坐50人,则空出一辆客车,并且有一辆还可以坐12人.下列五个方程:
①45m+28=50(m﹣1)﹣12; ②45m+28=50m﹣(12+50); ③![]() ;④
;④![]() ; ⑤45m+28=50(m﹣2)+38.其中正确的有( )
; ⑤45m+28=50(m﹣2)+38.其中正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个三角形数阵,仔细观察排列规律:
第1行 1
第2行 -![]()
![]()
第3行 -![]()
![]() -
-![]()
第4行 ![]() -
-![]()
![]() -
-![]()
.....
按照这个规律继续排列下去,第21行第2个数是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
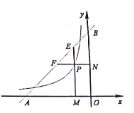
【题目】如图,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,点
,点![]() 是反比例函数
是反比例函数![]() 的图象上位于直线
的图象上位于直线![]() 下方的点,过点
下方的点,过点![]() 分别作
分别作![]() 轴、
轴、![]() 轴的垂线,垂足分别为点
轴的垂线,垂足分别为点![]() ,交直线
,交直线![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() 的值为__________.
的值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】让我们轻松一下,做一个数字游戏.第一步:取一个自然数![]() ,计算
,计算![]() 得
得![]() ;第二步:算出
;第二步:算出![]() 的各位数字之和得
的各位数字之和得![]() ,计算
,计算![]() 得
得![]() ;第三步:算出
;第三步:算出![]() 的各位数字之和得
的各位数字之和得![]() ,计算
,计算![]() 得
得![]() ;
;![]() 依此类推,则
依此类推,则![]() 的值为
的值为![]()
![]()
A.26B.65C.122D.123
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校“体育课外活动兴趣小组”,开设了以下体育课外活动项目:A.足球 B.乒乓球C.羽毛球 D.篮球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有 人,在扇形统计图中“D”对应的圆心角的度数为 ;
(2)请你将条形统计图补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加市里组织的乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的原始分均为100分.前6名选手的得分如下:
序号 项目 | 1 | 2 | 3 | 4 | 5 | 6 |
笔试成绩/分 | 85 | 92 | 84 | 90 | 84 | 80 |
面试成绩/分 | 90 | 88 | 86 | 90 | 80 | 85 |
根据规定,笔试成绩和面试成绩分别按一定的百分比折合成综合成绩(综合成绩的满分仍为100分).
(1)这6名选手笔试成绩的中位数是________分,众数是________分;
(2)现得知1号选手的综合成绩为88分,求笔试成绩和面试成绩各占的百分比;
(3)求出其余五名选手的综合成绩,并以综合成绩排序确定前两名人选.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是最大的负整数,
是最大的负整数,![]() 是
是![]() 的倒数,
的倒数,![]() 比
比![]() 小1,且
小1,且![]() 、
、![]() 、
、![]() 分别是点
分别是点![]() 、
、![]() 、
、![]() 在数轴上对应的数.若动点
在数轴上对应的数.若动点![]() 从点
从点![]() 出发沿数轴正方向运动,动点
出发沿数轴正方向运动,动点![]() 同时从点
同时从点![]() 出发沿数轴负方向运动,点
出发沿数轴负方向运动,点![]() 的速度是每秒3个单位长度,点
的速度是每秒3个单位长度,点![]() 的速度是每秒1个单位长度.
的速度是每秒1个单位长度.
![]()
(1)在数轴上标出点![]() 、
、![]() 、
、![]() 的位置;
的位置;
(2)运动前![]() 、
、![]() 两点之间的距离为 ;运动t秒后,点
两点之间的距离为 ;运动t秒后,点![]() ,点
,点![]() 运动的路程分别为 和 ;
运动的路程分别为 和 ;
(3)求运动几秒后,点![]() 与点
与点![]() 相遇?
相遇?
(4)在数轴上找一点![]() ,使点
,使点![]() 到
到![]() 、
、![]() 、
、![]() 三点的距离之和等于11,直接写出所有点
三点的距离之和等于11,直接写出所有点![]() 对应的数.
对应的数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com