
【题目】已知![]() 是最大的负整数,
是最大的负整数,![]() 是
是![]() 的倒数,
的倒数,![]() 比
比![]() 小1,且
小1,且![]() 、
、![]() 、
、![]() 分别是点
分别是点![]() 、
、![]() 、
、![]() 在数轴上对应的数.若动点
在数轴上对应的数.若动点![]() 从点
从点![]() 出发沿数轴正方向运动,动点
出发沿数轴正方向运动,动点![]() 同时从点
同时从点![]() 出发沿数轴负方向运动,点
出发沿数轴负方向运动,点![]() 的速度是每秒3个单位长度,点
的速度是每秒3个单位长度,点![]() 的速度是每秒1个单位长度.
的速度是每秒1个单位长度.
![]()
(1)在数轴上标出点![]() 、
、![]() 、
、![]() 的位置;
的位置;
(2)运动前![]() 、
、![]() 两点之间的距离为 ;运动t秒后,点
两点之间的距离为 ;运动t秒后,点![]() ,点
,点![]() 运动的路程分别为 和 ;
运动的路程分别为 和 ;
(3)求运动几秒后,点![]() 与点
与点![]() 相遇?
相遇?
(4)在数轴上找一点![]() ,使点
,使点![]() 到
到![]() 、
、![]() 、
、![]() 三点的距离之和等于11,直接写出所有点
三点的距离之和等于11,直接写出所有点![]() 对应的数.
对应的数.
【答案】(1)见解析;(2)6;3t;t.;(3)运动1.5秒后,点![]() 与点
与点![]() 相遇;(4)
相遇;(4)![]() 或
或![]()
【解析】
(1)按照整数、倒数的概念,确定a、b、c的值,并在数轴上表示出来即可;
(2)观察数轴可知运动前![]() 、
、![]() 两点之间的距离为AB,再利用路程=速度×时间,即可用含t的代数式表示点
两点之间的距离为AB,再利用路程=速度×时间,即可用含t的代数式表示点![]() ,点
,点![]() 运动的路程;
运动的路程;
(3)点![]() 与点
与点![]() 相遇,则点P运动路程与点Q运动路程的和为AB的长,列出方程,求解即可;
相遇,则点P运动路程与点Q运动路程的和为AB的长,列出方程,求解即可;
(4)分情况讨论:当点M在C点左侧时;当点M在A、C之间时;当点M在A、B之间时;当点M在B点右侧时;设点M表示的数是m,利用数轴上点之间的距离=大数减小数,列出方程求解,再根据情况取舍即可.
(1)![]() 是最大的负整数,则a=-1
是最大的负整数,则a=-1
![]() 是
是![]() 的倒数,则b=5
的倒数,则b=5
![]() 比
比![]() 小1,则c=-1-1=-2
小1,则c=-1-1=-2

(2)运动前![]() 、
、![]() 两点之间的距离为AB=5-(-1)=6
两点之间的距离为AB=5-(-1)=6
点P运动路程为3t,点Q运动路程为t,
故答案为:6;3t;t.
(3)点![]() 与点
与点![]() 相遇,则点P运动路程与点Q运动路程的和为6
相遇,则点P运动路程与点Q运动路程的和为6
即:3t+t=6,
解得:t=1.5
故:运动1.5秒后,点![]() 与点
与点![]() 相遇;
相遇;
(4)设点M表示的数是m,
当点M在C点左侧时,MC+MA+MB=-2-m+(-1)-m+5-m=11
解得:![]() ,
,
所以,点![]() 对应的数为
对应的数为![]() ;
;
当点M在A、C之间时,MC+MA+MB=m-(-2)+(-1)-m+5-m=11
解得:![]() (舍去);
(舍去);
当点M在A、B之间时,MC+MA+MB=m-(-2)+m-(-1)+5-m=11
解得:![]() ,
,
所以,点![]() 对应的数为
对应的数为![]()
当点M在B点右侧时,MC+MA+MB= m-(-2)+m-(-1)+m-5=11
解得:![]() (舍去),
(舍去),
所以点![]() 对应的数为
对应的数为![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
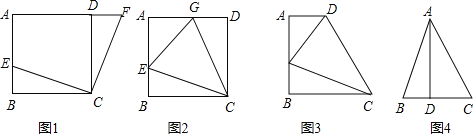
【题目】(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下列两题:
①如图3,在四边形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=12,E是AB上一点,且∠DCE=45°,BE=4,则DE= .
②如图4,在△ABC中,∠BAC=45°,AD⊥BC,且BD=2,AD=6,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,AF,BE是△ABC的中线, AF⊥BE , 垂足为P.像△ABC这样的三角形均为“中垂三角形”.设![]()
![]() ,
,![]() ,
,![]() .
.

特例探索
(1)如图1,当∠![]() =45°,
=45°,![]() 时,
时,![]() = ,
= ,![]() ;
;
如图2,当∠![]() =30°,
=30°,![]() 时,
时, ![]() = ,
= ,![]() ;
;
归纳证明
(2)请你观察(1)中的计算结果,猜想![]() 三者之间的关系,用等式表示出来,
三者之间的关系,用等式表示出来,
并利用图3证明你发现的关系式;
拓展应用
(3)如图4,在□ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG, AD=![]() ,AB=6.
,AB=6.
求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少?”,共有4个选项:
A.1.5小时以上 B.1~1.5小时 C.0.5~1小时 D.0.5小时以下
图1、2是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:
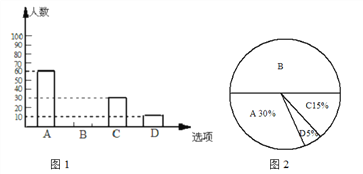
(1)本次一共调查了____名学生;学生参加体育活动时间的中位数落在_____时间段(填写上面所给“A”、“B”、“C”、“D”中的一个选项);
(2)在图1中将选项B的部分补充完整;
(3)若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机王师傅某天上午的营运全是在经十路上进行的,如果规定向东为正,向西为负,他这天上午所接十位乘客的行车里程(单位:千米)如下:
+5、-2、+5、-1、+10、-3、-2、+12、+4、-5.
(1)王师傅这天上午的出发地记为0,他将最后一名乘客送抵目的地时,距上午的出发地有多远?
(2)若出租车消耗天然气量为0.1立方米/千米,这天上午王师傅共耗天然气多少立方米?
(3)若出租车起步价为9元,起步里程为3千米(包括3千米),超过部分(不足1千米按1千米计算)每千米1.5元,这天上午王师傅共得车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.
 试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一串有黑有白,其排列有一定规律的珠子,被盒子遮住一部分(如图),则这串珠子被盒子遮住的部分(包括白色和黑色)共有( )颗.
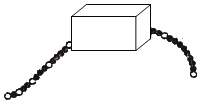
A.16B.18C.20D.22
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,AB=2AD,DE平分∠ADC,交AB于点E,交CB的延长线于点F,EG∥AD交DC于点G.
中,AB=2AD,DE平分∠ADC,交AB于点E,交CB的延长线于点F,EG∥AD交DC于点G.
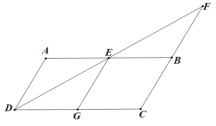
⑴求证:四边形AEGD为菱形;
⑵若![]() ,AD=2,求DF的长.
,AD=2,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点O是直线AB上一点,OC、OD为从点O引出的两条射线,∠BOD=30°,∠COD=![]() ∠AOC.
∠AOC.
(1)如图①,求∠AOC的度数;
(2)如图②,在∠AOD的内部作∠MON=90°,请直接写出∠AON与∠COM之间的数量关系 ;
(3)在(2)的条件下,若OM为∠BOC的角平分线,试说明∠AON=∠CON.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com