
分析 (1)先把实际问题转化成数学问题后,就是求出h=-5t2+10t的顶点坐标即可;
(2)因为-5<0,抛物线开口向下,有最大值,根据顶点坐标公式表示函数的最大值,根据题目对最大值的要求,求待定系数v0.
解答 解:(1)当v0=10m/s时,
h=-5t2+10t
=-5(t2-2t+1)+5,
=-5(t-1)2+5,
∵a=-5<0,
∴图象的开口向下,有最大值,
当t=1时,h最大值=5
当t=1s时,小球最高,小球运动中的最大高度是5m;
(2)h=-5t2+v0•t,其对称轴为t=-$\frac{{v}_{0}}{2×(-5)}$=$\frac{{v}_{0}}{10}$.
当t=$\frac{{v}_{0}}{10}$时,h最大=-5•($\frac{{v}_{0}}{10}$)2+v0•$\frac{{v}_{0}}{10}$=$\frac{{{v}_{0}}^{2}}{20}$=20,
整理得:v02=400,
∴v0=20,或v0=-20(舍去)
答:喷水的速度应该达到20m/s.
点评 本题考查了二次函数的实际应用,解此题的关键是把实际问题转化成数学问题,利用二次函数的性质就能求出结果.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
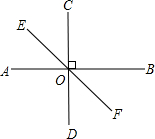 如图,直线AB、EF相交于O点,CD⊥AB于O点,∠EOD=130°,则∠BOF的度数为( )
如图,直线AB、EF相交于O点,CD⊥AB于O点,∠EOD=130°,则∠BOF的度数为( )| A. | 30° | B. | 40° | ||
| C. | 50° | D. | 以上结果均不正确 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
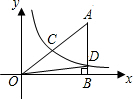 在直角坐标系中,有如图所示的Rt△ABO,AB⊥x轴于点B,斜边AO=10,sin∠AOB=$\frac{3}{5}$,反比例函数y=$\frac{k}{x}$(k>0)的图象经过AO的中点C,且与AB交于点D,则tan∠DOB的值为$\frac{3}{16}$.
在直角坐标系中,有如图所示的Rt△ABO,AB⊥x轴于点B,斜边AO=10,sin∠AOB=$\frac{3}{5}$,反比例函数y=$\frac{k}{x}$(k>0)的图象经过AO的中点C,且与AB交于点D,则tan∠DOB的值为$\frac{3}{16}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
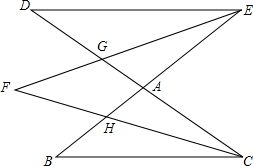 如图,DC和BE相交于点A,EF平分∠DEA,CF平分∠ACB,EF,CF分别与AD,AB交于点G,H,请猜想∠F与∠B,∠D之间的数量关系,并证明你的结论.
如图,DC和BE相交于点A,EF平分∠DEA,CF平分∠ACB,EF,CF分别与AD,AB交于点G,H,请猜想∠F与∠B,∠D之间的数量关系,并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
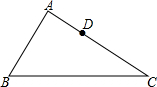 如图,△ABC中,AB=12,AC=15,D为AC上一点,CD=$\frac{2}{3}$AC,在AB边上找一点E,使得△ADE与△ABC相似,求AE的长.
如图,△ABC中,AB=12,AC=15,D为AC上一点,CD=$\frac{2}{3}$AC,在AB边上找一点E,使得△ADE与△ABC相似,求AE的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com