
【题目】已知正比例函数y=k1x的图象与反比例函数y= ![]() 的图象的一个交点是(2,3).
的图象的一个交点是(2,3).
(1)求出这两个函数的表达式;
(2)作出两个函数的草图,利用你所作的图形,猜想并验证这两个函数图象的另一个交点的坐标;
(3)直接写出使反比例函数值大于正比例函数值的x的取值范围.
【答案】
(1)解:由正比例函数y=k1x的图象与反比例函数y= ![]() 的图象的一个交点是(2,3),得
的图象的一个交点是(2,3),得
3=2k1,3= ![]() .
.
解得k1= ![]() ,k2=6.
,k2=6.
正比例函数y= ![]() x;反比例函数y=
x;反比例函数y= ![]() ;
;
(2)解:画出函数的图象如图:
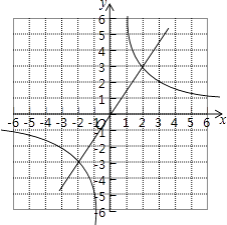
两个函数图象的一个交点的坐标(2,3),猜想另一个交点的坐标(﹣2,﹣3),
把(﹣2,﹣3)代入y= ![]() 成立;
成立;
(3)解:由图象可知:比例函数值大于正比例函数值的x的取值范围是x<﹣2或0<x<2.
【解析】(1)由已知两个函数交点是(2,3),由待定系数法易得两个函数解析式为正比例函数y= ![]() x;反比例函数y=
x;反比例函数y=![]() ;
;
(2)做草图时注意可以找几个关键点,尽量做得准确,由于正比例函数和反比例函数均为中心对称图形,所以易得另一个交点为(﹣2,﹣3)代入解析式验证即可。
(3)首先确定交点位置,根据交点把x轴分成四段,再根据上边图像的函数值大于下边图像的函数值,容易确定比例函数值大于正比例函数值的x的取值范围是x<﹣2或0<x<2
【考点精析】本题主要考查了反比例函数的图象的相关知识点,需要掌握反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】甲、乙两同学用一副扑克牌中牌面数字分别是:3,4,5,6的4张牌做抽数学游戏.游戏规则是:将这4张牌的正面全部朝下,洗匀,从中随机抽取一张,抽得的数作为十位上的数字,然后,将所抽的牌放回,正面全部朝下、洗匀,再从中随机抽取一张,抽得的数作为个位上的数字,这样就得到一个两位数.若这个两位数小于45,则甲获胜,否则乙获胜.你认为这个游戏公平吗?请运用概率知识说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,如图为边长为a的大正方形中有一个边长为b的小正方形,如图是由如图中阴影部分拼成的一个长方形.

(1)设如图中阴影部分面积为S1,如图中阴影部分面积为S2,请用含a、b的代数式表示:![]() ____ __,
____ __,![]() ___ ___(只需表示,不必化简);
___ ___(只需表示,不必化简);
(2)以上结果可以验证哪个乘法公式?
请写出这个乘法公式__ ____;
(3)利用(2)中得到的公式,
计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两枚正四面体骰子的各面上分别标有数字1,2,3,4,现在同时投掷这两枚骰子,并分别记录着地的面所得的点数为a、b.
(1)假设两枚正四面体都是质地均匀,各面着地的可能性相同,请你在下面表格内列举出所有情形(例如(1,2),表示a=1,b=2),并求出两次着地的面点数相同的概率.
b | 1 | 2 | 3 | 4 |
1 | (1,2) | |||
2 | ||||
3 | ||||
4 |
(2)为了验证试验用的正四面体质地是否均匀,小明和他的同学取一枚正四面体进行投掷试验.试验中标号为1的面着地的数据如下:
试验总次数 | 50 | 100 | 150 | 200 | 250 | 600 |
“标号1”的面着地的次数 | 15 | 26 | 34 | 48 | 63 | 125 |
“标号1”的面着地的频率 | 0.3 | 0.26 | 0.23 | 0.24 |
请完成表格(数字精确到0.01),并根据表格中的数据估计“标号1的面着地”的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了更好地开展球类运动,体育组决定用1600元购进足球8个和篮球14个,并且篮球的单价比足球的单价多20元,请解答下列问题:
(1)求出足球和篮球的单价;
(2)若学校欲用不超过3240元,且不少于3200元再次购进两种球50个,求出有哪几种购买方案?
(3)在(2)的条件下,若已知足球的进价为50元,篮球的进价为65元,则在第二次购买方案中,哪种方案商家获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写推理的依据。
(1)已知:AB∥CD,AD∥BC。求证:∠B=∠D。
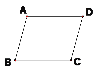
证明:∵AB∥CD,AD∥BC( 已知 )
∴∠A+∠B=180,∠A+∠D=180°(_______________________________)
∴∠B=∠D (___________________________)
(2)已知:DF∥AC,∠A=∠F。求证:AE∥BF。
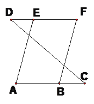
证明:∵DF∥AC (已知)
∴∠FBC=∠_______(_______________________________)
∵∠A=∠F(已知)
∴∠A=∠FBC (____________________)
∴AE∥FB (_____________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com