
【题目】两根木条,一根长60cm,另一根长80cm,将它们的一端重合,放在同一直线上,此时两根木条的中点间的距离是 cm.
【答案】70或10.
【解析】
试题设AB=60cm,BC=80cm,AB中点为点M,BC中点为点N,两线段重合的端点为点B.分两种情况讨论:①点A、点C在点B两侧时,此时MN=BM+BN;②点A、点C在点B同侧时,此时MN=BN-BM.
解:设AB=60cm,BC=80cm,AB中点为点M,BC中点为点N,两线段重合的端点为点B.
①点A、点C在点B两侧时,如图:
![]()
则BM=![]() AB=30cm,BN=
AB=30cm,BN=![]() BC=40cm,
BC=40cm,
则MN=BM+BN=30+40=70cm.
②点A、点C在点B同侧时,如图:
![]()
则BM=![]() AB=30cm,BN=
AB=30cm,BN=![]() BC=40cm,
BC=40cm,
则MN=BN-BM=40-30=10cm.
故答案为70cm或10cm.


科目:初中数学 来源: 题型:
【题目】某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围为![]() ~
~![]() 的产品为合格〉.随机各抽取了20个祥品迸行检测.过程如下:
的产品为合格〉.随机各抽取了20个祥品迸行检测.过程如下:
收集数据(单位:![]() ):
):
甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180.
乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183.
整理数据:
组别频数 | 165.5~170.5 | 170.5~175.5 | 175.5~180.5 | 180.5~185.5 | 185.5~190.5 | 190.5~195.5 |
甲车间 | 2 | 4 | 5 | 6 | 2 | 1 |
乙车间 | 1 | 2 |
|
| 2 | 0 |
分析数据:
车间 | 平均数 | 众数 | 中位数 | 方差 |
甲车间 | 180 | 185 | 180 | 43.1 |
乙车间 | 180 | 180 | 180 | 22.6 |
应用数据;
(1)计算甲车间样品的合格率.
(2)估计乙车间生产的1000个该款新产品中合格产品有多少个?
(3)结合上述数据信息.请判断哪个车间生产的新产品更好.并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线 ![]() 与x轴交于点A,B,与y轴负半轴交于点C且OB=OC,点P为抛物线上的一个动点,且点P位于x轴下方,点P与点C不重合。
与x轴交于点A,B,与y轴负半轴交于点C且OB=OC,点P为抛物线上的一个动点,且点P位于x轴下方,点P与点C不重合。
(1)求抛物线的解析式
(2)若△PAC的面积为 ![]() ,求点P的坐标
,求点P的坐标
(3)若以A、B、C、P为顶点的四边形面积记作S,则S取何值时,对应的点P有且只有2个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数y=k1x的图象与反比例函数y= ![]() 的图象的一个交点是(2,3).
的图象的一个交点是(2,3).
(1)求出这两个函数的表达式;
(2)作出两个函数的草图,利用你所作的图形,猜想并验证这两个函数图象的另一个交点的坐标;
(3)直接写出使反比例函数值大于正比例函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的是( )
A.方程x2-4x+2=0无实数根;
B.两条对角线互相垂直且相等的四边形是正方形
C.甲、乙、丙三人站成一排合影留念,则甲、乙二人相邻的概率是 ![]()
D.若 ![]() 是反比例函数,则k的值为2或-1。
是反比例函数,则k的值为2或-1。
查看答案和解析>>
科目:初中数学 来源: 题型:
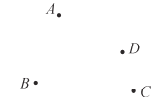
【题目】读句画图:如图所示,A,B,C,D在同一平面内.
(1)过点A和点D画直线;
(2)画射线CD;
(3)连接AB;
(4)连接BC,并反向延长BC.
(5)已知AB=9,直线AB上有一点F,并且BF=3,则AF=_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y= ![]() (x﹥0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是 .
(x﹥0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是 . 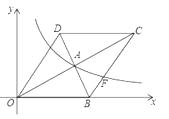
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点A(1,0)、B(3,1)、C(3,3);反比例函数 ![]() (x>0)的图象经过点D,点P是一次函数 y=kx+33k (k≠0)的图象与该反比例函数图象的一个公共点.
(x>0)的图象经过点D,点P是一次函数 y=kx+33k (k≠0)的图象与该反比例函数图象的一个公共点.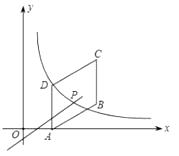
(1)求反比例函数的关系式;
(2)通过计算:说明一次函数 y=kx+33k 的图象一定经过点C;
(3)当一次函数 y=kx+33k 的图象平分平行四边形ABCD的面积时,求此一次函数的关系式。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“十一”国庆节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)设每件童装降价x元时,每天可销售件,每件盈利元;(用x的代数式表示)
(2)每件童装降价多少元时,平均每天赢利1200元.
(3)要想平均每天赢利2000元,可能吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com