
【题目】如图,四边形ABCD是平行四边形,点A(1,0)、B(3,1)、C(3,3);反比例函数 ![]() (x>0)的图象经过点D,点P是一次函数 y=kx+33k (k≠0)的图象与该反比例函数图象的一个公共点.
(x>0)的图象经过点D,点P是一次函数 y=kx+33k (k≠0)的图象与该反比例函数图象的一个公共点.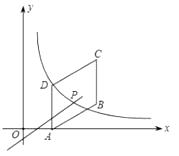
(1)求反比例函数的关系式;
(2)通过计算:说明一次函数 y=kx+33k 的图象一定经过点C;
(3)当一次函数 y=kx+33k 的图象平分平行四边形ABCD的面积时,求此一次函数的关系式。
【答案】
(1)解:∵ 四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵A(1,0)、B(3,1)、C(3,3),
∴D(1,2),
∵D(1,2)在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴m=1×2=2,
∴反比例函数的关系式为 ![]() (x>0).
(x>0).
(2)解:∵C(3,3),
∴3k+33k =3.
∴一次函数 y=kx+33k 的图象一定经过点C.
(3)解:∵ 一次函数 y=kx+33k 的图象平分平行四边形ABCD的面积,
∴一次函数 y=kx+33k 的图象经过点A,
又∵ A(1,0),
∴ k+33k=0 ,
∴k=![]() .
.
∴一次函数的关系式为: y=![]() x
x![]() .
.
【解析】(1)由平行四边形的性质得AD∥BC,AD=BC;又知A(1,0)、B(3,1)、C(3,3),从而得出D(1,2),再由D(1,2)在反比例函数图象上,从而求出m的值.
(2)将点C(3,3)坐标代入一次函数解析式,从而得出一次函数 y=kx+33k 的图象一定经过点C.
(3)由一次函数 y=kx+33k 的图象平分平行四边形ABCD的面积,从而得出一次函数 y=kx+33k 的图象经过点A;再将A(1,0)点坐标代入一次函数解析式,从而得k的值,即可得出一次函数解析式.
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法,以及对平行四边形的性质的理解,了解平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.


科目:初中数学 来源: 题型:
【题目】填写推理的依据。
(1)已知:AB∥CD,AD∥BC。求证:∠B=∠D。
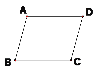
证明:∵AB∥CD,AD∥BC( 已知 )
∴∠A+∠B=180,∠A+∠D=180°(_______________________________)
∴∠B=∠D (___________________________)
(2)已知:DF∥AC,∠A=∠F。求证:AE∥BF。
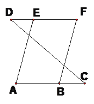
证明:∵DF∥AC (已知)
∴∠FBC=∠_______(_______________________________)
∵∠A=∠F(已知)
∴∠A=∠FBC (____________________)
∴AE∥FB (_____________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是直线AB上一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.

(1)指出图中∠AOD与∠BOE的补角;
(2)试判断∠COD与∠COE具有怎样的数量关系.并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
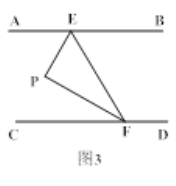
【题目】如图,AB∥CD,定点E,F分别在直线AB,CD上,平行线AB,CD之间有一动点P.
(1)如图1,当P点在EF的左侧时,∠AEP,∠EPF,∠PFC满足数量关系为 ,如图2,当P点在EF的右侧时,∠AEP,∠EPF,∠PFC满足数量关系为 .
(2)如图3,当∠EPF=90°,FP平分∠EFC时,求证:EP平分∠AEF;
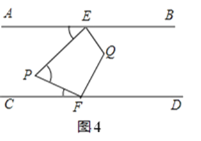
(3)如图4,QE,QF分别平分∠PEB和∠PFD,且点P在EF左侧.
①若∠EPF=60°,则∠EQF= .
②猜想∠EPF与∠EQF的数量关系,并说明理由;
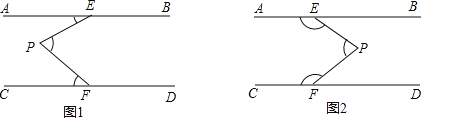
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县城要铺一条自来水管道,决定由甲、乙两个工程队来完成这一工程,已知甲工程队比乙工程队每天多铺10m,且甲工程队铺设350m所用的天数与乙工程队铺设250m所用的天数相同![]() 甲、乙两个工程队每天各能铺设多少米管道?
甲、乙两个工程队每天各能铺设多少米管道?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com