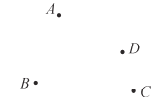
【题目】读句画图：如图所示，A，B，C，D在同一平面内．
（1）过点A和点D画直线；
（2）画射线CD；
（3）连接AB；
（4）连接BC，并反向延长BC．
（5）已知AB=9，直线AB上有一点F，并且BF=3，则AF=_________
科目：初中数学 来源： 题型：
【题目】如图1，在矩形ABCD中，动点P从点B出发，沿BC﹣CD﹣DA运动至点A停止，设点P运动的路程为x，△ABP的面积为y．如果y关于x的函数图象如图2所示，则△ABC的面积是 ． 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，如图为边长为a的大正方形中有一个边长为b的小正方形，如图是由如图中阴影部分拼成的一个长方形．
（1）设如图中阴影部分面积为S1，如图中阴影部分面积为S2，请用含a、b的代数式表示：
____ __，
___ ___(只需表示，不必化简)；
（2）以上结果可以验证哪个乘法公式？
请写出这个乘法公式__ ____；
（3）利用（2）中得到的公式，
计算：
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校为了更好地开展球类运动，体育组决定用1600元购进足球8个和篮球14个，并且篮球的单价比足球的单价多20元，请解答下列问题：
（1）求出足球和篮球的单价；
（2）若学校欲用不超过3240元，且不少于3200元再次购进两种球50个，求出有哪几种购买方案？
（3）在（2）的条件下，若已知足球的进价为50元，篮球的进价为65元，则在第二次购买方案中，哪种方案商家获利最多？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】填写推理的依据。
（1）已知：AB∥CD，AD∥BC。求证：∠B=∠D。
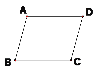
证明：∵AB∥CD，AD∥BC（ 已知 ）
∴∠A+∠B=180，∠A+∠D=180°（_______________________________）
∴∠B=∠D （___________________________）
（2）已知：DF∥AC，∠A=∠F。求证：AE∥BF。
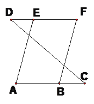
证明：∵DF∥AC （已知）
∴∠FBC=∠_______（_______________________________）
∵∠A=∠F（已知）
∴∠A=∠FBC （____________________）
∴AE∥FB （_____________________________）
查看答案和解析>>
科目：初中数学 来源： 题型：
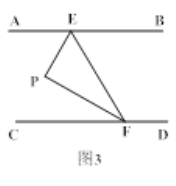
【题目】如图，AB∥CD，定点E，F分别在直线AB，CD上，平行线AB，CD之间有一动点P．
（1）如图1，当P点在EF的左侧时，∠AEP，∠EPF，∠PFC满足数量关系为 ，如图2，当P点在EF的右侧时，∠AEP，∠EPF，∠PFC满足数量关系为 ．
（2）如图3，当∠EPF＝90°，FP平分∠EFC时，求证：EP平分∠AEF；
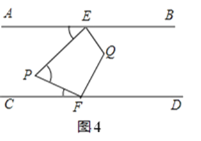
（3）如图4，QE，QF分别平分∠PEB和∠PFD，且点P在EF左侧．
①若∠EPF＝60°，则∠EQF＝ ．
②猜想∠EPF与∠EQF的数量关系，并说明理由；
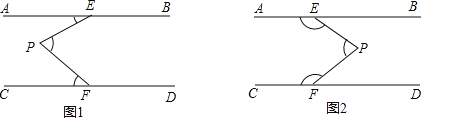
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】填空，将理由补充完整．
如图，
于
，
于
，
，求证：
．
证明：∵，（已知）
∴
（垂直的定义）
∴
（________________________）
∴
（________________________）
∵（已知）
又∵
（________________________）
∴
（________________________）
∴
（________________________）
∴（________________________）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
