
【题目】填空,将理由补充完整.
如图,![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() ,求证:
,求证:![]() .
.

证明:∵![]() ,
,![]() (已知)
(已知)
∴![]() (垂直的定义)
(垂直的定义)
∴![]() (________________________)
(________________________)
∴![]() (________________________)
(________________________)
∵![]() (已知)
(已知)
又∵![]() (________________________)
(________________________)
∴![]() (________________________)
(________________________)
∴![]() (________________________)
(________________________)
∴![]() (________________________)
(________________________)
【答案】同位角相等,两直线平行;两直线平行,同位角相等;平角的定义;等量代换;等量代换;内错角相等,两直线平行
【解析】
由垂直的定义得出∠BED=∠BFC=90°;由同位角相等得出ED∥FC;由两直线平行,同位角相等,得出∠2=∠3;由∠1+∠EDC=180°,∠2+∠EDC=180°,等量代换得出∠1=∠2,等量代换得出∠1=∠3;由内错角相等,两直线平行即可得出结论.
证明:∵CF⊥AB,DE⊥AB(已知),
∴∠BED=∠BFC=90°(垂直的定义),
∴ED∥FC (同位角相等,两直线平行),
∴∠2=∠3 (两直线平行,同位角相等),
∵∠1+∠EDC=180°(已知),
又∵∠2+∠EDC=180°(平角的定义),
∴∠1=∠2 (等量代换),
∴∠1=∠3(等量代换),
∴FG∥BC (内错角相等,两直线平行).
故答案为:同位角相等,两直线平行;两直线平行,同位角相等;平角的定义;等量代换;等量代换;内错角相等,两直线平行.


科目:初中数学 来源: 题型:
【题目】读句画图:如图所示,A,B,C,D在同一平面内.
(1)过点A和点D画直线;
(2)画射线CD;
(3)连接AB;
(4)连接BC,并反向延长BC.
(5)已知AB=9,直线AB上有一点F,并且BF=3,则AF=_________
查看答案和解析>>
科目:初中数学 来源: 题型:
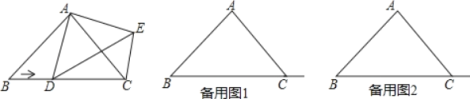
【题目】如图,△ABC中,∠ACB=90°,DC=AE,AE是BC边上的中线,过点C作CF⊥AE,垂足为点F,过点B作BD⊥BC交CF的延长线于点D.
(1)求证:AC=CB; (2)若AC=12 cm,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,完成下列推理过程.
已知:DE⊥AO于E,BO⊥AO,∠CFB=∠EDO.
证明:CF∥DO.

证明:∵DE⊥AO,BO⊥AO(已知)
∴∠DEA=∠BOA=90°( )
∴DE∥BO( )
∴∠EDO=∠DOF( )
又∵∠CFB=∠EDO( ④ )
∴∠DOF=∠CFB( ⑤ )
∴CF∥DO( ⑥ )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“十一”国庆节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)设每件童装降价x元时,每天可销售件,每件盈利元;(用x的代数式表示)
(2)每件童装降价多少元时,平均每天赢利1200元.
(3)要想平均每天赢利2000元,可能吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知直线y=﹣![]() x+4与x轴、y轴分别交于A、B两点,点C(0,n)是y轴上一点.把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标为______.
x+4与x轴、y轴分别交于A、B两点,点C(0,n)是y轴上一点.把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已等腰Rt△ABC中,∠BAC=90°.点D从点B出发沿射线BC移动,以AD为腰作等腰Rt△ADE,∠DAE=90°.连接CE.
(1)如图,求证:△ACE≌△ABD;
(2)点D运动时,∠BCE的度数是否发生变化?若不变化,求它的度数;若变化,说明理由;
(3)若AC=![]() ,当CD=1时,请直接写出DE的长.
,当CD=1时,请直接写出DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生开展跳绳比赛活动,每班派5名学生参加,按团体总分多少排列名次,统计发现成绩最好的甲班和乙班总分相等,下表是甲班和乙班学生的比赛数据![]() 单位:个
单位:个![]()
选手 | 1号 | 2号 | 3号 | 4号 | 5号 | 总计 |
甲班 | 100 | 98 | 105 | 94 | 103 | 500 |
乙班 | 99 | 100 | 95 | 109 | 97 | 500 |
此时有学生建议,可以通过考察数据中的其他信息作为参考,请解答下列问题:
![]() 求两班比赛数据中的中位数,以及方差;
求两班比赛数据中的中位数,以及方差;
![]() 请根据以上数据,说明应该定哪一个班为冠军?为什么?
请根据以上数据,说明应该定哪一个班为冠军?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,G是正方形形ABCD的边BC上一点,DE、BF分别垂直AG于点E、F,则图中与△ABF相似的三角形有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com