【题目】如图，△ABC中，∠ACB＝90°，DC＝AE，AE是BC边上的中线，过点C作CF⊥AE，垂足为点F，过点B作BD⊥BC交CF的延长线于点D.
(1)求证：AC＝CB； (2)若AC＝12 cm，求BD的长．
寒假乐园北京教育出版社系列答案科目：初中数学 来源： 题型：
【题目】如图，如图为边长为a的大正方形中有一个边长为b的小正方形，如图是由如图中阴影部分拼成的一个长方形．
（1）设如图中阴影部分面积为S1，如图中阴影部分面积为S2，请用含a、b的代数式表示：
____ __，
___ ___(只需表示，不必化简)；
（2）以上结果可以验证哪个乘法公式？
请写出这个乘法公式__ ____；
（3）利用（2）中得到的公式，
计算：
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】填写推理的依据。
（1）已知：AB∥CD，AD∥BC。求证：∠B=∠D。
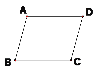
证明：∵AB∥CD，AD∥BC（ 已知 ）
∴∠A+∠B=180，∠A+∠D=180°（_______________________________）
∴∠B=∠D （___________________________）
（2）已知：DF∥AC，∠A=∠F。求证：AE∥BF。
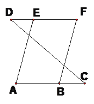
证明：∵DF∥AC （已知）
∴∠FBC=∠_______（_______________________________）
∵∠A=∠F（已知）
∴∠A=∠FBC （____________________）
∴AE∥FB （_____________________________）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB∥CD，定点E，F分别在直线AB，CD上，平行线AB，CD之间有一动点P．
（1）如图1，当P点在EF的左侧时，∠AEP，∠EPF，∠PFC满足数量关系为 ，如图2，当P点在EF的右侧时，∠AEP，∠EPF，∠PFC满足数量关系为 ．
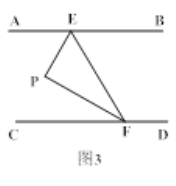
（2）如图3，当∠EPF＝90°，FP平分∠EFC时，求证：EP平分∠AEF；
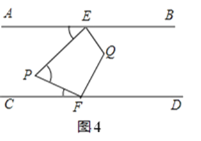
（3）如图4，QE，QF分别平分∠PEB和∠PFD，且点P在EF左侧．
①若∠EPF＝60°，则∠EQF＝ ．
②猜想∠EPF与∠EQF的数量关系，并说明理由；
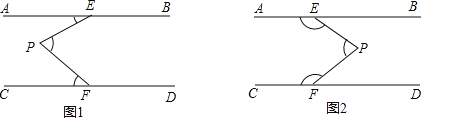
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知
，点
是射线
上一动点(与点
不重合)，
分别平分
和
，分别交射线于点
若点运动到某处时，恰有
，此时
与
有何位置关系?请说明理由．
在点运动的过程中，
与
之间的关系是否发生变化?若不变，请写出它们的关系并说明理由；若变化，请写出变化规律．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，AD=5，AB=8，点E为射线DC上一个动点，把△ADE沿直线AE折叠，当点D的对应点F刚好落在线段AB的垂直平分线上时，则DE的长为 ． 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】填空，将理由补充完整．
如图，
于
，
于
，
，求证：
．
证明：∵，（已知）
∴
（垂直的定义）
∴
（________________________）
∴
（________________________）
∵（已知）
又∵
（________________________）
∴
（________________________）
∴
（________________________）
∴（________________________）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知∠1=∠3，CD∥EF，试说明∠1=∠4．请将过程填写完整．
解：∵∠1=∠3，
又∠2=∠3(_______)，
∴∠1=____，
∴______∥______(_______)，
又∵CD∥EF，
∴AB∥_____，
∴∠1=∠4(两直线平行，同位角相等).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
