
【题目】如图,已知∠1=∠3,CD∥EF,试说明∠1=∠4.请将过程填写完整.

解:∵∠1=∠3,
又∠2=∠3(_______),
∴∠1=____,
∴______∥______(_______),
又∵CD∥EF,
∴AB∥_____,
∴∠1=∠4(两直线平行,同位角相等).
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,DC=AE,AE是BC边上的中线,过点C作CF⊥AE,垂足为点F,过点B作BD⊥BC交CF的延长线于点D.
(1)求证:AC=CB; (2)若AC=12 cm,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
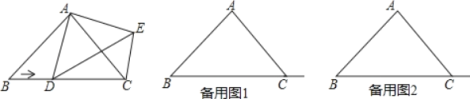
【题目】已等腰Rt△ABC中,∠BAC=90°.点D从点B出发沿射线BC移动,以AD为腰作等腰Rt△ADE,∠DAE=90°.连接CE.
(1)如图,求证:△ACE≌△ABD;
(2)点D运动时,∠BCE的度数是否发生变化?若不变化,求它的度数;若变化,说明理由;
(3)若AC=![]() ,当CD=1时,请直接写出DE的长.
,当CD=1时,请直接写出DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生开展跳绳比赛活动,每班派5名学生参加,按团体总分多少排列名次,统计发现成绩最好的甲班和乙班总分相等,下表是甲班和乙班学生的比赛数据![]() 单位:个
单位:个![]()
选手 | 1号 | 2号 | 3号 | 4号 | 5号 | 总计 |
甲班 | 100 | 98 | 105 | 94 | 103 | 500 |
乙班 | 99 | 100 | 95 | 109 | 97 | 500 |
此时有学生建议,可以通过考察数据中的其他信息作为参考,请解答下列问题:
![]() 求两班比赛数据中的中位数,以及方差;
求两班比赛数据中的中位数,以及方差;
![]() 请根据以上数据,说明应该定哪一个班为冠军?为什么?
请根据以上数据,说明应该定哪一个班为冠军?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,AB=4,且∠ABC=∠ABE=60°,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM,则AM+BM+CM的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于某一函数给出如下定义:若存在实数p,当其自变量的值为p时,其函数值等于p,则称p为这个函数的不变值.在函数存在不变值时,该函数的最大不变值与最小不变值之差q称为这个函数的不变长度.特别地,当函数只有一个不变值时,其不变长度q为零.例如:下图中的函数有0,1两个不变值,其不变长度q等于1.
(1)分别判断函数y=x-1,y=x-1,y=x2有没有不变值?如果有,直接写出其不变长度;
(2)函数y=2x2-bx. ①若其不变长度为零,求b的值;
②若1≤b≤3,求其不变长度q的取值范围;
(3)记函数y=x2-2x(x≥m)的图象为G1 , 将G1沿x=m翻折后得到的函数图象记为G2 , 函数G的图象由G1和G2两部分组成,若其不变长度q满足0≤q≤3,则m的取值范围为.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,G是正方形形ABCD的边BC上一点,DE、BF分别垂直AG于点E、F,则图中与△ABF相似的三角形有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知第三象限的点P(x,y)满足![]() ,
,![]() .
.
(1)求点P的坐标;
(2)①点P到x轴的距离为_______;
②把点P向右平移m个单位后得到P1,则点P1到x轴的距离为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com