Question

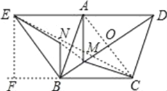
【题目】如图，四边形ABCD是菱形，AB＝4，且∠ABC＝∠ABE＝60°，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM，则AM+BM+CM的最小值为_____．

Answer 1

【答案】

【解析】

根据“两点之间线段最短”，当M点位于BD与CE的交点处时，AM+BM+CM的值最小，即等于EC的长．

如图，连接MN，∵△ABE是等边三角形，

∴BA=BE，∠ABE=60°．

∵∠MBN=60°，

∴∠MBN﹣∠ABN=∠ABE﹣∠ABN．

即∠MBA=∠NBE．

又∵MB=NB，

∴△AMB≌△ENB（SAS），

∴AM=EN，

∵∠MBN=60°，MB=NB，

∴△BMN是等边三角形．

∴BM=MN．

∴AM+BM+CM=EN+MN+CM．

根据“两点之间线段最短”，得EN+MN+CM=EC最短

∴当M点位于BD与CE的交点处时，AM+BM+CM的值最小，即等于EC的长，

过E点作EF⊥BC交CB的延长线于F，

∴∠EBF=180°﹣120°=60°，

∵BC=4，

∴BF=2，EF=2，在Rt△EFC中，

∵EF2+FC2=EC2，

EC=4．

故答案为：4.