
【题目】如图,已知![]() ,点
,点![]() 是射线
是射线![]() 上一动点(与点
上一动点(与点![]() 不重合),
不重合),![]() 分别平分
分别平分![]() 和
和![]() ,分别交射线
,分别交射线![]() 于点
于点![]()
![]()
![]() 若点
若点![]() 运动到某处时,恰有
运动到某处时,恰有![]() ,此时
,此时![]() 与
与![]() 有何位置关系?请说明理由.
有何位置关系?请说明理由.
![]() 在点
在点![]() 运动的过程中,
运动的过程中,![]() 与
与![]() 之间的关系是否发生变化?若不变,请写出它们的关系并说明理由;若变化,请写出变化规律.
之间的关系是否发生变化?若不变,请写出它们的关系并说明理由;若变化,请写出变化规律.

【答案】(1)60°;(2)![]() ,证明详见解析;(3)不变,
,证明详见解析;(3)不变,![]() ,理由详见解析
,理由详见解析
【解析】
(1)由平行线的性质可得∠ABN=120°,即∠ABP+∠PBN=120°,再根据角平分线的定义知∠ABP=2∠CBP、∠PBN=2∠DBP,可得2∠CBP+2∠DBP=120°,即∠CBD=∠CBP+∠DBP=60°;
(2)由AM∥BN得∠ACB=∠CBN,当∠ACB=∠ABD时有∠CBN=∠ABD,得∠ABC+∠CBD=∠CBD+∠DBN,即∠ABC=∠DBN,再根据角平分线的定义可得![]() ,最后根据∠ABN=120°可得
,最后根据∠ABN=120°可得![]() ,进而可得答案;
,进而可得答案;
(3)由AM∥BN得∠APB=∠PBN、∠ADB=∠DBN,根据BD平分∠PBN知∠PBN=2∠DBN,从而可得∠APB=2∠ADB.
解:(1)∵AM∥BN,∠A=60°,
∴∠A+∠ABN=180°,
∴∠ABN=120°;
∵AM∥BN,
∴∠ABN+∠A=180°,
∴∠ABN=180°﹣60°=120°,
∴∠ABP+∠PBN=120°,
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP,∠PBN=2∠DBP,
∴2∠CBP+2∠DBP=120°,
∴∠CBD=∠CBP+∠DBP=60°;
![]()
理由:![]()
![]()
![]()
![]()
![]() ,
,
即![]()
![]() 分别平分
分别平分![]() 和
和![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
即![]()
![]() 不变.且
不变.且![]()
理由:![]()
![]()
![]() 平分
平分![]()
![]()
![]()


科目:初中数学 来源: 题型:
【题目】探索题:
![]()
![]()
![]()
![]()
根据前面的规律,回答下列问题:
(1)![]() =__________;
=__________;
(2)当x=4时,![]() ;
;
(3)求:![]() 的值。(请写出解题过程);
的值。(请写出解题过程);
(4)求:![]() 的值的个位数字。(只写答案)。
的值的个位数字。(只写答案)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
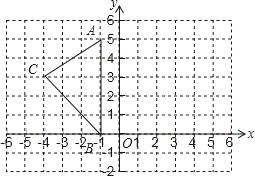
【题目】如图:在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)S△ABC= .
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1(其中点A、B、C的对称点分别为点A1、B1、C1).
(3)写出点A1、B1、C1的坐标.A1 ,B1 ,C1 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,DC=AE,AE是BC边上的中线,过点C作CF⊥AE,垂足为点F,过点B作BD⊥BC交CF的延长线于点D.
(1)求证:AC=CB; (2)若AC=12 cm,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
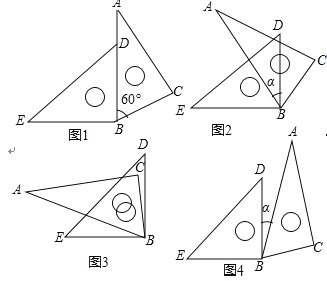
【题目】图1是由一副三角板拼成的图案,其中![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求图1中![]() 的度数;
的度数;
(2)若将图1中的三角板![]() 不动,将另一三角板
不动,将另一三角板![]() 绕点
绕点![]() 顺时针或逆时针旋转
顺时针或逆时针旋转![]() 度(
度(![]() ).当
).当![]() 时,求
时,求![]() 的度数(图2,图3,图4仅供参考).
的度数(图2,图3,图4仅供参考).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,完成下列推理过程.
已知:DE⊥AO于E,BO⊥AO,∠CFB=∠EDO.
证明:CF∥DO.

证明:∵DE⊥AO,BO⊥AO(已知)
∴∠DEA=∠BOA=90°( )
∴DE∥BO( )
∴∠EDO=∠DOF( )
又∵∠CFB=∠EDO( ④ )
∴∠DOF=∠CFB( ⑤ )
∴CF∥DO( ⑥ )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知直线y=﹣![]() x+4与x轴、y轴分别交于A、B两点,点C(0,n)是y轴上一点.把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标为______.
x+4与x轴、y轴分别交于A、B两点,点C(0,n)是y轴上一点.把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,AB=4,且∠ABC=∠ABE=60°,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM,则AM+BM+CM的最小值为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com