
【题目】已知AB是⊙O的直径,弦CD与AB相交,∠BAC=38°.
(1)如图①,若D为弧AB的中点,求∠ABC和∠ABD的大小;
(2)如图②,过点D作⊙O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的大小.
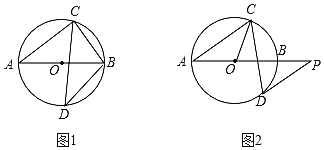
【答案】(1)∠ABC=52°,∠ABD=45°;(2)∠OCD=26°.
【解析】
(1)根据圆周角和圆心角的关系和图形可以求得∠ABC和∠ABD的大小;
(2)根据题意和平行线的性质、切线的性质可以求得∠OCD的大小.
(1)∵AB是⊙O的直径,弦CD与AB相交,∠BAC=38°,∴∠ACB=90°,∴∠ABC=∠ACB﹣∠BAC=90°﹣38°=52°.
∵D为![]() 的中点,∠AOB=180°,∴∠AOD=90°,∴∠ABD=45°;
的中点,∠AOB=180°,∴∠AOD=90°,∴∠ABD=45°;
(2)连接OD.
∵DP切⊙O于点D,∴OD⊥DP,即∠ODP=90°,由DP∥AC,又∠BAC=38°,∴∠P=∠BAC=38°.
∵∠AOD是△ODP的一个外角,∴∠AOD=∠P+∠ODP=128°,∴∠ACD=64°.
∵OC=OA,∠BAC=38°,∴∠OCA=∠BAC=38°,∴∠OCD=∠ACD﹣∠OCA=64°﹣38°=26°.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热[此过程中水温y(℃)与开机时间x(分)满足一次函数关系],当加热到100℃时自动停止加热,随后水温开始下降[此过程中水温y(℃)与开机时间x(分)成反比例关系],当水温降至20℃时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
(1)当0≤x≤8时,求水温y(℃)与开机时间x(分)的函数关系式;
(2)求图中t的值;
(3)若小明在通电开机后即外出散步,请你预测小明散步45分钟回到家时,饮水机内的温度约为多少℃?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线与直线的图象如图所示,则下列说法:
①当0<x<2时, y1>y2;②y1随x的增大而增大的取值范围是x<2;③使得y2大于4的x值不存在;④若y1=2,则x=2﹣![]() 或x=1.其中正确的有( )
或x=1.其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
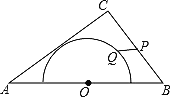
【题目】如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P、Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
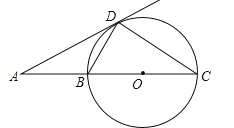
【题目】如图,BC是⊙O的直径,AD是⊙O的切线,切点为D,AD与CB的延长线交于点A,∠C=30°,给出下面四个结论:①AD=DC;②AB=BD;③AB=![]() BC;④BD=CD,
BC;④BD=CD,
其中正确的个数为( )
A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα=![]() =
=![]() ,根据上述角的余切定义,解下列问题:
,根据上述角的余切定义,解下列问题:
(1)如图1,若BC=3,AB=5,则ctanB= ;
(2)ctan60°= ;
(3)如图2,已知:△ABC中,∠B是锐角,ctan C=2,AB=10,BC=20,试求∠B的余弦cosB的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知常数a(a是整数)满足下面两个要求:
①关于x的一元二次方程ax2+3x﹣1=0有两个不相等的实数根;
②反比例函数y=![]() 的图象在二,四象限.
的图象在二,四象限.
(1)求a的值;
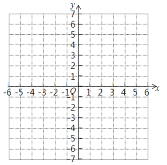
(2)在所给直角坐标系中用描点法画出y=![]() 的图象,并根据图象写出:
的图象,并根据图象写出:
当x>4时,y的取值范围 ;
当y<1时,x的取值范围是.
查看答案和解析>>
科目:初中数学 来源: 题型:
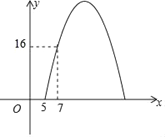
【题目】某商场经调研得出某种商品每天的利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx﹣75,其图象如图所示.
(1)求a与b的值;
(2)销售单价为多少元时,该种商品每天的销售利润最大?最大利润是多少元?(参考公式:当x=![]() 时,二次函数y=ax2+bx+c(a≠0)有最小(大)值)
时,二次函数y=ax2+bx+c(a≠0)有最小(大)值)
(3)销售单价定在多少时,该种商品每天的销售利润为21元?结合图象,直接写出销售单价定在什么范围时,该种商品每天的销售利润不低于21元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com