
【题目】我们规定在网格内的某点进行一定条件操作到达目标点:H代表所有的水平移动,H1代表向右水平移动1个单位长度,H-1代表向左平移1个单位长度;S代表上下移动,S1代表向上移动1个单位长度,S-1代表向下移动1个单位长度,![]() 表示点P在网格内先一次性水平移动,在此基础上再一次性上下移动;
表示点P在网格内先一次性水平移动,在此基础上再一次性上下移动;![]() 表示点P在网格内先一次性上下移动,在此基础上再一次性水平移动.
表示点P在网格内先一次性上下移动,在此基础上再一次性水平移动.
(1)如图,在网格中标出![]() 移动后所到达的目标点
移动后所到达的目标点![]() ;
;

(2)如图,在网格中的点B到达目标点A,写出点B的移动方法________________;

(3)如图,在网格内有格点线段AC,现需要由点A出发,到达目标点D,使得A、C、D三点构成的格点三角形是等腰直角三角形,在图中标出所有符合条件的点D的位置并写出点A的移动方法.

【答案】(1)见解析;(2)![]() 或
或![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)根据题意,![]() 表示点A先向右水平移动1个单位,再向上移动2个单位,据此即可标出点
表示点A先向右水平移动1个单位,再向上移动2个单位,据此即可标出点![]() ;
;
(2)由点B到达目标点A,可以先向下移动3个单位,再向左水平移动2个单位,或先向左水平移动2个单位,再向下移动3个单位,据此解答即可;
(3)先找出全部符合题意的点D,再根据点的位置写出移动方法即可.
解:(1)目标点![]() 的位置如图1所示;
的位置如图1所示;
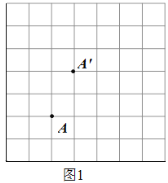
(2)由点B到达目标点A,可以先向下移动3个单位,再向左水平移动2个单位,或先向左水平移动2个单位,再向下移动3个单位,所以点B的移动方法是:![]() 或
或![]() ;
;
故答案为:![]() 或
或![]() ;
;
(3)如图2所示,使得A、C、D三点构成的格点三角形是等腰直角三角形的点D共有5个,分别是:D1、D2、D3、D4、D5;
∴A到D1的移动方法是:![]() 或
或![]() ;
;
A到D2的移动方法是:![]() 或
或![]() ;
;
A到D3的移动方法是:![]() 或
或![]() ;
;
A到D4的移动方法是:![]() 或
或![]() ;
;
A到D5的移动方法是:![]() 或
或![]() .
.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=65时,y=55;x=75时,y=45.
(1)求一次函数y=kx+b的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.
(1)证明:∠BAC=∠DAC.
(2)若∠BEC=∠ABE,试证明四边形ABCD是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(k﹣1)x2﹣2kx+k+2=0有两个不相等的实数根.
(1)求k的取值范围;
(2)若x1,x2是一元二次方程的两个实数根,且满足![]() =﹣2,求k的值,并求此时方程的解.
=﹣2,求k的值,并求此时方程的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于△ABC及其边上的点P,给出如下定义:如果点![]() ,
,![]() ,
,![]() ,……,
,……,![]() 都在△ABC的边上,且
都在△ABC的边上,且![]() ,那么称点
,那么称点![]() ,
,![]() ,
,![]() ,……,
,……,![]() 为△ABC关于点P的等距点,线段
为△ABC关于点P的等距点,线段![]() ,
,![]() ,
,![]() ,……,
,……,![]() 为△ABC关于点P的等距线段.
为△ABC关于点P的等距线段.
(1)如图1,△ABC中,∠A<90°,AB=AC,点P是BC的中点.

①点B,C △ABC关于点P的等距点,线段PA,PB △ABC关于点P的等距线段;(填“是”或“不是”)
②△ABC关于点P的两个等距点![]() ,
,![]() 分别在边AB,AC上,当相应的等距线段最短时,在图1中画出线段
分别在边AB,AC上,当相应的等距线段最短时,在图1中画出线段![]() ,
,![]() ;
;
(2)△ABC是边长为4的等边三角形,点P在BC上,点C,D是△ABC关于点P的等距点,且PC=1,求线段DC的长;
(3)如图2,在Rt△ABC中,∠C=90°,∠B=30°.点P在BC上,△ABC关于点P的等距点恰好有四个,且其中一个是点![]() .若
.若![]() ,直接写出
,直接写出![]() 长的取值范围.(用含
长的取值范围.(用含![]() 的式子表示)
的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC 中,点 D 是线段 BC 上一点.作射线 AD ,点 B 关于射线 AD 的对称点为 E .连接 EC 并延长,交射线 AD 于点 F .
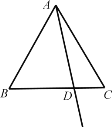
(1)补全图形;(2)求∠AFE 的度数;(3)用等式表示线段 AF 、CF 、 EF 之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是本地区一种产品30天的销售图象,产品日销售量y(单位:件)与时间t(单位:天)的大致函数关系如图①,图②是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列结论错误的是( )

A. 日销售量为150件的是第12天与第30天
B. 第10天销售一件产品的利润是15元
C. 从第1天到第20天这段时间内日销售利润将先增加再减少
D. 第18天的日销售利润是1225元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
![]() 年上半年出台规定,将用空气质量指数替代原有的空气污染指数.空气质量按照空气质量指数大小分为六级,相对应空气质量的六个类别,指数越大、级别越高,说明污染的情况越严重,对人体的健康危害也就越大,从一级优,二级良,三级轻度污染,四级中度污染,直至五级重度污染,六级严重污染.将空气质量达到一级优,二级良的天气定义为达标天气.
年上半年出台规定,将用空气质量指数替代原有的空气污染指数.空气质量按照空气质量指数大小分为六级,相对应空气质量的六个类别,指数越大、级别越高,说明污染的情况越严重,对人体的健康危害也就越大,从一级优,二级良,三级轻度污染,四级中度污染,直至五级重度污染,六级严重污染.将空气质量达到一级优,二级良的天气定义为达标天气.
北京市环保局![]() 年
年![]() 月
月![]() 日上午向媒体通报:
日上午向媒体通报:
![]() 年北京空气质量状况,与
年北京空气质量状况,与![]() 年相比,
年相比,![]() 年,北京各项污染物同比均有所改善.据报导,
年,北京各项污染物同比均有所改善.据报导,![]() 年北京空气质量持续改善,
年北京空气质量持续改善,![]() 年均浓度
年均浓度![]() 微克/立方米,同比下降
微克/立方米,同比下降![]() ,但是这一数值依旧超出国家标准
,但是这一数值依旧超出国家标准![]() .
.![]() 年,北京空气质量达标天数
年,北京空气质量达标天数![]() 天,较
天,较![]() 年增加
年增加![]() 天,其中
天,其中![]() 一级优的天数增加了
一级优的天数增加了![]() 天,
天,![]() 年北京有重污染天(含严重污染天)
年北京有重污染天(含严重污染天)![]() 天.其中
天.其中![]() 年
年![]() 月至
月至![]() 月底,北京全市
月底,北京全市![]() 浓度同比下降
浓度同比下降![]() ,空气质量达标天数较去年同期增加
,空气质量达标天数较去年同期增加![]() 天,空气重污染天数同比减少
天,空气重污染天数同比减少![]() 年本市空气质量达标天数较
年本市空气质量达标天数较![]() 年增加
年增加![]() 天,其中PM2.5一级优的天数增加了
天,其中PM2.5一级优的天数增加了![]() 天.
天.![]() 年本市
年本市![]() 重污染天(含严重污染天)数占全年总天数的
重污染天(含严重污染天)数占全年总天数的![]() ,其中在
,其中在![]() 月中发生重污染
月中发生重污染![]() 天,占
天,占![]() 月和
月和![]() 月天数的
月天数的![]() ,与
,与![]() 年同期相比增加
年同期相比增加![]() 天.
天.![]() 年北京市
年北京市![]() 一级优的天数达到
一级优的天数达到![]() 天,较
天,较![]() 年减少了
年减少了![]() 天,但
天,但![]() 导致的重污染天(含严重污染天)数明显减少了
导致的重污染天(含严重污染天)数明显减少了![]() 天,从
天,从![]() 年的
年的![]() 天下降为
天下降为![]() 天.
天.
根据以下材料解答下列问题:
(![]() )
)![]() 年本市空气质量达标天数为__________天;
年本市空气质量达标天数为__________天;![]() 年平均浓度的国家标准限值是__________微克/立方米;(结果保留整数).
年平均浓度的国家标准限值是__________微克/立方米;(结果保留整数).
(![]() )选择统计表或统计图,将
)选择统计表或统计图,将![]() 年
年![]() 一级优天数的情况表示出来;预估
一级优天数的情况表示出来;预估![]() 年北京市
年北京市![]() 一级优天数约__________天.
一级优天数约__________天.
(![]() )小明从报道中发现“
)小明从报道中发现“![]() 年
年![]() 月至
月至![]() 月底,北京全市
月底,北京全市![]() 浓度同比下降
浓度同比下降![]() ,空气质量达标天数较去年同期增加
,空气质量达标天数较去年同期增加![]() 天,空气重污染天数同比减少
天,空气重污染天数同比减少![]() 天,”他由此推断“
天,”他由此推断“![]() 年全年的
年全年的![]() 达标天数的年增长率将比
达标天数的年增长率将比![]() 年全年的
年全年的![]() 达标天数的年增长率出现大幅增长,”你同意他的结论吗?并说明你的理由.
达标天数的年增长率出现大幅增长,”你同意他的结论吗?并说明你的理由.
(![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,长方形![]() 的项点
的项点![]() 的坐标是
的坐标是![]() .
.

(1)直接写出![]() 点坐标(______,______),
点坐标(______,______),![]() 点坐标(______,______);
点坐标(______,______);
(2)如图,D为![]() 中点.连接
中点.连接![]() ,
,![]() ,如果在第二象限内有一点
,如果在第二象限内有一点![]() ,且四边形
,且四边形![]() 的面积是
的面积是![]() 面积的
面积的![]() 倍,求满足条件的点
倍,求满足条件的点![]() 的坐标;
的坐标;

(3)如图,动点![]() 从点
从点![]() 出发,以每钞
出发,以每钞![]() 个单位的速度沿线段
个单位的速度沿线段![]() 运动,同时动点
运动,同时动点![]() 从点
从点![]() 出发.以每秒
出发.以每秒![]() 个单位的連度沿线段
个单位的連度沿线段![]() 运动,当
运动,当![]() 到达
到达![]() 点时,
点时,![]() ,
,![]() 同时停止运动,运动时间是
同时停止运动,运动时间是![]() 秒
秒![]() ,在
,在![]() ,
,![]() 运动过程中.当
运动过程中.当![]() 时,直接写出时间
时,直接写出时间![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com