
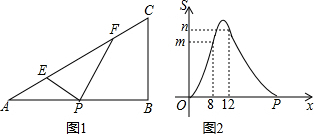
分析 (1)根据0<x≤8和8<x≤12的函数的解析式不同可知:AP=8,AB=12,作等腰△AEP的高线EG,证明△AEG∽△ACB,求出BC的长;
(2)先求出∠A=30°,及直角△PEF的各内角的度数,分三种情况进行讨论:
①当0<x≤8时,如图2,△PEF与△ABC重合的部分是△PEF,
②当8<x≤12时,如图3,△PEF与△ABC重合的部分是四边形CEPH,
③先根据图4求出p的值,当12<x<24时,如图5,△PEF与△ABC重合的部分是△ECM,
分别代入面积公式求解即可.
解答 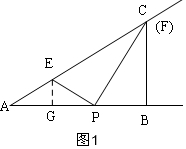 解:(1)如图1,根据0<x≤8和8<x≤12的函数的解析式不同可知:
解:(1)如图1,根据0<x≤8和8<x≤12的函数的解析式不同可知:
AP=8,AB=12,
∴PB=12-8=4,
过E作EG⊥AB于G,则∠AGE=90°,
∵AE=EP,
∴AG=PG=4,
∵∠B=90°,
∴∠B=∠AGE,
∴EG∥BC,
∴△AEG∽△ACB,
∴$\frac{AE}{AB}=\frac{EG}{BC}$=$\frac{4}{12}$=$\frac{1}{3}$,
设EG=a,则BC=3a,
∵PE⊥PF,
∴∠EPF=90°,
∴∠EPG+∠BPF=90°,
∵∠EPG+∠PEG=90°,
∴∠BPF=∠PEG,
∵∠B=∠PGE=90°,
∴△PEG∽△CPB,
∴$\frac{PG}{BC}=\frac{EG}{PB}$,
∴$\frac{4}{3a}$=$\frac{a}{4}$,
3a2=16,
a=±$\frac{4\sqrt{3}}{3}$,
∵a>0,
∴a=$\frac{4\sqrt{3}}{3}$,
∴BC=3a=4$\sqrt{3}$,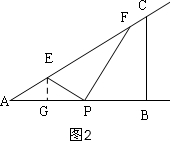
故答案为:4$\sqrt{3}$;
(2)由勾股定理得:AC=$\sqrt{1{2}^{2}+(4\sqrt{3})^{2}}$=8$\sqrt{3}$,
∴AC=2BC,
∴∠A=30°,
∵AE=EP,
∴∠A=∠EPA=30°,
∴∠FEP=60°,
∴∠EFP=30°,
分三种情况: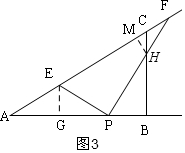
①当0<x≤8时,如图2,△PEF与△ABC重合的部分是△PEF,
过E作EG⊥AB于G,
则AG=$\frac{1}{2}$x,
cos30°=$\frac{AG}{AE}$,
∴AE=$\frac{AG}{cos30°}$=$\frac{\frac{1}{2}x}{\frac{\sqrt{3}}{2}}$=$\frac{\sqrt{3}}{3}$x,
∴PE=AE=$\frac{\sqrt{3}}{3}$x,
在Rt△EPF中,tan30°=$\frac{PE}{PF}$,
∴PF=$\frac{PE}{tan30°}$=$\frac{\frac{\sqrt{3}}{3}x}{\frac{\sqrt{3}}{3}}$=x,
∴S=S△PEF=$\frac{1}{2}$PE•PF=$\frac{1}{2}$×$\frac{\sqrt{3}}{3}$x2=$\frac{\sqrt{3}}{6}{x}^{2}$;
②当8<x≤12时,如图3,△PEF与△ABC重合的部分是四边形CEPH,
过E作E作EG⊥AB于G,过H作HM⊥AC于M,
AE=PE=$\frac{\sqrt{3}}{3}$x,PF=x,
∴EC=AC-AE=8$\sqrt{3}$-$\frac{\sqrt{3}}{3}$x,
∴FC=EF-EC=$\frac{2\sqrt{3}}{3}$x-(8$\sqrt{3}$-$\frac{\sqrt{3}}{3}$x)=$\sqrt{3}$x-8$\sqrt{3}$,
∵∠F=30°,∠ACB=60°,
∴∠F=∠CHF=30°,
∴CH=FC=$\sqrt{3}$x-8$\sqrt{3}$,
∴sin60°=$\frac{MH}{CH}$,
MH=CH•sin60°=$\frac{\sqrt{3}}{2}$($\sqrt{3}$x-8$\sqrt{3}$)=$\frac{3}{2}$x-12,
∴S=S△DEF-S△CHF=$\frac{\sqrt{3}}{6}{x}^{2}$-$\frac{1}{2}$($\sqrt{3}$x-8$\sqrt{3}$)($\frac{3}{2}x$-12)=-$\frac{7\sqrt{3}}{12}{x}^{2}$+12$\sqrt{3}$x-48$\sqrt{3}$;
③如图4,当E与C重合时,S=0,此时x=AP=2AB=24,即p=24,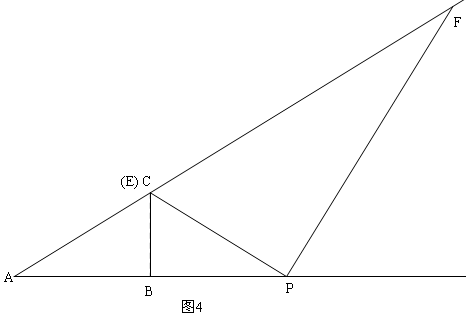
当12<x<24时,如图5,△PEF与△ABC重合的部分是△ECM,
∵AC=8$\sqrt{3}$,AE=$\frac{\sqrt{3}}{3}$x,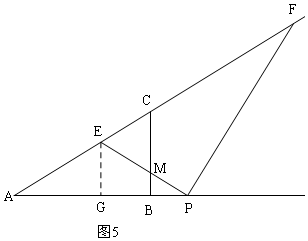
∴EC=8$\sqrt{3}$-$\frac{\sqrt{3}}{3}$x,
∵∠EMC=∠BMP=60°,∠ACB=60°,
∴△ECM是等边三角形,
∴CM=EC=8$\sqrt{3}$-$\frac{\sqrt{3}}{3}$x,
∵AB=12,AG=$\frac{1}{2}$x,
∴BG=12-$\frac{1}{2}$x,
∴S=S△ECM=$\frac{1}{2}$CM•BG=$\frac{1}{2}$(8$\sqrt{3}$-$\frac{\sqrt{3}}{3}$x)(12-$\frac{1}{2}$x)=$\frac{\sqrt{3}}{12}{x}^{2}-4\sqrt{3}x+48\sqrt{3}$;
综上所述,S关于x的函数解析式为:
S=$\left\{\begin{array}{l}{\frac{\sqrt{3}}{6}{x}^{2}(0<x≤8)}\\{-\frac{7\sqrt{3}}{12}{x}^{2}+12\sqrt{3}x-48\sqrt{3}(8<x≤12)}\\{\frac{\sqrt{3}}{12}{x}^{2}-4\sqrt{3}x+48\sqrt{3}(12<x<24)}\end{array}\right.$.
点评 本题考查了动点问题的函数图象,有难度,需要认真理解两个图形中标记的数字的含义,如本题中的8和12的意义是关键,对于重叠部分的面积,先确定其特殊位置,再分情况进行讨论,代入面积公式即可求出相应的解析式.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:解答题
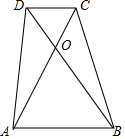 如图,在梯形ABCD中.DC∥AB.对角线AC,BD交于O点,设S△ODC=S1,S△AOB=S2,求证:S梯形ABCD=($\sqrt{{S}_{1}}$+$\sqrt{{S}_{2}}$)2.
如图,在梯形ABCD中.DC∥AB.对角线AC,BD交于O点,设S△ODC=S1,S△AOB=S2,求证:S梯形ABCD=($\sqrt{{S}_{1}}$+$\sqrt{{S}_{2}}$)2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点C、D在线段AB上,且△PCD是边长为1的等边三角形.
如图,点C、D在线段AB上,且△PCD是边长为1的等边三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,点A在y轴的正半轴上,点B在x轴的负半轴上,△ABC为等腰直角三角形,AC=BC,CD⊥x轴于点D,连接DE交AB于点M,若D(a,0)E(0,b),且满足b2+2ab+2b2-12b+36=0
如图,在平面直角坐标系中,点A在y轴的正半轴上,点B在x轴的负半轴上,△ABC为等腰直角三角形,AC=BC,CD⊥x轴于点D,连接DE交AB于点M,若D(a,0)E(0,b),且满足b2+2ab+2b2-12b+36=0查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com