
分析 设3x+5=t,原方程变形为t2-2t-8=0,利用因式分解法解得t1=4,t2=-2,然后求出对应的x的值即可.
解答 解:设3x+5=t,
原方程变形为t2-2t-8=0,
(t-4)(t+2)=0,
解得t1=4,t2=-2,
当t=4时,3x+5=4,解得x=-$\frac{1}{3}$;
当t=-2时,3x+5=-2,解得x=-$\frac{7}{3}$,
所以原方程的解为x1=-$\frac{1}{3}$,x2=-$\frac{7}{3}$.
点评 本题考查了换元法解以一元二次方程:们常用的是整体换元法,是在已知或者未知中,某个代数式几次出现,而用一个字母来代替它从而简化问题,当然有时候要通过变形才能发现.把一些形式复杂的方程通过换元的方法变成一元二次方程,从而达到降次的目的.


科目:初中数学 来源: 题型:选择题
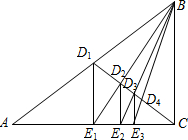 如图,已知Rt△ABC的面积为1,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连接BE1交CD1于D2;过D2作D2E2⊥AC于E2,连接BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点D4,D5,…,Dn,分别记△BD1E1,△BD2E2,△BD3E3,…,△BDnEn的面积为S1,S2,S3,…Sn.则Sn等于( )
如图,已知Rt△ABC的面积为1,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连接BE1交CD1于D2;过D2作D2E2⊥AC于E2,连接BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点D4,D5,…,Dn,分别记△BD1E1,△BD2E2,△BD3E3,…,△BDnEn的面积为S1,S2,S3,…Sn.则Sn等于( )| A. | $\frac{1}{(n+1)^{2}}$ | B. | $\frac{1}{(2n)^{2}}$ | C. | $\frac{1}{4n}$ | D. | $\frac{1}{{2}^{n+1}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 用40cm长的绳子围成矩形ABCD,设AB=xm,矩形ABCD的面积为S(m2)
用40cm长的绳子围成矩形ABCD,设AB=xm,矩形ABCD的面积为S(m2)| x | … | 8 | 9 | 9.5 | 10 | 10.5 | 11 | 12 | … |
| S | … | 96 | 99 | 99.75 | 100 | 99,75 | 99 | 96 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com