
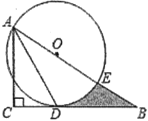
【题目】如图,已知在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D,以AB上点O为圆心作⊙O,使⊙O经过点A和点D.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AE=6,劣弧DE的长为π,求线段BD,BE与劣弧DE所围成的阴影部分的面积(结果保留根号和π).
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
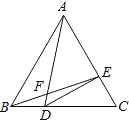
【题目】如图,△ABC 是等边三角形,点 D、E 分别在 BC、AC 上,且 BD=![]() BC,CE=
BC,CE= ![]() AC,BE、AD 相交于点 F,连接 DE, 则下列结论:①∠AFE=60°;②DE⊥AC;③CE2=DFDA;④AFBE=AEAC,正确的结论有( )
AC,BE、AD 相交于点 F,连接 DE, 则下列结论:①∠AFE=60°;②DE⊥AC;③CE2=DFDA;④AFBE=AEAC,正确的结论有( )
A.①②③B.①②④C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组要测量一栋五层居民楼CD的高度,该楼底层为车库,高2.5米;上面五层居住,每层高度相等,测角仪支架离地1.5米,在A处测得五楼顶部点D的仰角为60°,在B处测得四楼顶部点E的仰角为30°,AB=14米,求居民楼的高度.(精确到0.1米,参考数据:![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着互联网的不断发展,移动支付的普及率越来越高,人们在购物时可选择的付款方式越来越多样化.为了解人们购物时常用付款方式,在某步行街进行了随机抽样调查,根据调查结果绘制以下两幅不完整统计图,请结合图中所给信息解答下列问题:
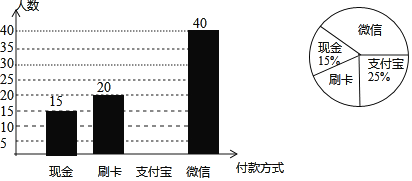
(1)此次共调查了 人,表示常用“微信”付款方式的扇形圆心角度数为 ,并补全条形统计图.
(2)该步行街某天的人流量约为2.4万人,其中约有50%的人参与购物,根据调查获得的信息,估计在这一天购物时用“微信”付款方式的人数为多少万人?
(3)若甲、乙两人在购物时,选择“现金”、“刷卡”、“支付宝”、“微信”(分别用A、B、C、D表示)付款的可能性相同.请通过列表或画树形图的方法,求两人在购物时,用同一种付款方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC纸板中,AC=4,BC=8,AB=11,P是BC上一点,沿过点P的直线剪下一个与△ABC相似的小三角形纸板,如果有4种不同的剪法,那么CP长的取值范围是( )
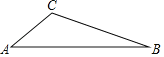
A.0<CP≤1B.0<CP≤2C.1≤CP<8D.2≤CP<8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解深圳市初中学生课外阅读情况,调查小组对该市这学期初中学生阅读课外书籍的册数进行了抽样调查,并根据调查结果绘制成如下统计图.
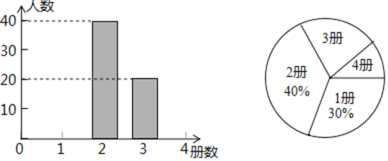
根据统计图提供的信息,解答下列问题:
(1)本次抽样调查的样本容量是 ;
(2)补全条形统计图;
(3)该市共有218000名初中生,估计该市初中学生这学期课外阅读超过2册的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() 和点C,与y轴交于点B,
和点C,与y轴交于点B,![]() 的面积是6.
的面积是6.
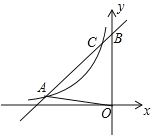
(1)求一次函数与反比例函数的表达式;(2)当![]() 时,比较
时,比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() ,其自变量的取值范围是
,其自变量的取值范围是![]() .当
.当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(1)根据给定的条件,求出![]() 的函数解析式;
的函数解析式;
(2)根据你所求的函数解析式,选取适当的自变量![]() 完成如表,并在下面的平面直角坐标系中描点并画出函数的大致图象:
完成如表,并在下面的平面直角坐标系中描点并画出函数的大致图象:
![]()
(3)请画出![]() 的图象,并结合图象直接写出:当
的图象,并结合图象直接写出:当![]() 时,
时,![]() 的取值范围是 .
的取值范围是 .
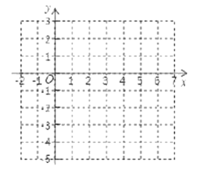
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】名闻遐迩的秦顺明前茶,成本每斤500元,某茶场今年春天试营销,每周的销售量y(斤)与销售单价x(元/斤)满足的关系如下表:
x(元/斤) | 550 | 600 | 650 | 680 | 700 |
y(斤) | 450 | 400 | 350 | 320 | 300 |
(1)请根据表中的数据猜想并写出y与x之间的函数关系式;
(2)若销售每斤茶叶获利不能超过40%,该茶场每周获利w元,试写w与x之间的函数关系式,并求出茶场每周的最大利润.
(3)若该茶场每周获利不少于40000元,试确定销售单价x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com