
【题目】名闻遐迩的秦顺明前茶,成本每斤500元,某茶场今年春天试营销,每周的销售量y(斤)与销售单价x(元/斤)满足的关系如下表:
x(元/斤) | 550 | 600 | 650 | 680 | 700 |
y(斤) | 450 | 400 | 350 | 320 | 300 |
(1)请根据表中的数据猜想并写出y与x之间的函数关系式;
(2)若销售每斤茶叶获利不能超过40%,该茶场每周获利w元,试写w与x之间的函数关系式,并求出茶场每周的最大利润.
(3)若该茶场每周获利不少于40000元,试确定销售单价x的取值范围.
【答案】(1)y=﹣x+1000;(2)w=﹣(x﹣750)2+62500,最大利润为60000元;(3)600≤x≤900
【解析】
(1)利用待定系数法求解可得一次函数解析式;
(2)根据“总利润=每斤的利润×周销售量”可得函数解析式,再利用二次函数的性质结合x的取值范围可得答案;
(3)求出w=40000时x的值,利用二次函数的性质可得.
解:(1)设y与x之间的函数关系式为y=kx+b,
根据题意,得:![]() ,
,
解得:![]() ,
,
则y=﹣x+1000;
(2)w=(x﹣500)(﹣x+1000)
=﹣x2+600x﹣500000,
=﹣(x﹣750)2+62500,
∵x﹣500≤500×40%,即x≤700,
∴当x=700时,w取得最大值,最大值为60000,即最大利润为60000元.
(3)当w=40000时,﹣(x﹣750)2+62500=40000,
解得:x=900或x=600,
∵a=﹣1,
∴当![]() 时,600≤x≤900.
时,600≤x≤900.
∴该茶场每周获利不少于40000元,销售单价x的取值范围为600≤x≤900.


科目:初中数学 来源: 题型:
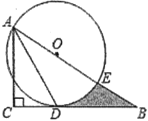
【题目】如图,已知在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D,以AB上点O为圆心作⊙O,使⊙O经过点A和点D.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AE=6,劣弧DE的长为π,求线段BD,BE与劣弧DE所围成的阴影部分的面积(结果保留根号和π).
查看答案和解析>>
科目:初中数学 来源: 题型:
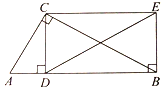
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D ,BE⊥AB,垂足为B,BE=CD连接CE,DE.
(1)求证:四边形CDBE是矩形
(2)若AC=2 ,∠ABC=30°,求DE的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在锐角![]() 中,
中,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 按逆时针方向旋转,得到
按逆时针方向旋转,得到![]() .
.
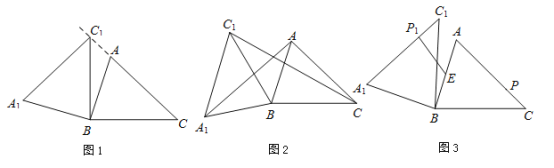
(1)如图1,当点![]() 在线段
在线段![]() 的延长线上时,求
的延长线上时,求![]() 的度数;
的度数;
(2)如图2,连接![]() ,
,![]() .若
.若![]() 的面积为4,求
的面积为4,求![]() 的面积;
的面积;
(3)如图3,点![]() 为线段
为线段![]() 中点,点
中点,点![]() 是线段
是线段![]() 上的动点,在
上的动点,在![]() 绕点
绕点![]() 按逆时针方向旋转过程中,点
按逆时针方向旋转过程中,点![]() 的对应点是点
的对应点是点![]() ,求线段
,求线段![]() 长度的最小值.
长度的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=![]() 在第一象限的图象经过点B,则OA2﹣AB2=_____.
在第一象限的图象经过点B,则OA2﹣AB2=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围为176mm~185mm的产品为合格),随机各抽取了20个样品进行检测,过程如下:
收集数据:(单位:mm)
甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180
乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183
整理数据:
频数 组别 | 165.5~170.5 | 170.5~175.5 | 175.5~180.5 | 180.5~185.5 | 185.5~190.5 | 190.5~195.5 |
甲车间 | 2 | 4 | 5 | 6 | 2 | 1 |
乙车间 | 1 | 2 | a | 6 | 2 | 0 |
分析数据:
车间 | 平均数 | 众数 | 中位数 | 方差 |
甲车间 | 180 | 185 | 180 | 43.1 |
乙车间 | 180 | 180 | 180 | 22.6 |
应用数据:
(1)计算甲车间样品的合格率;
(2)估计乙车间生产的8000个该款新产品中合格产品有多少个?
(3)结合上述数据信息,请判断哪个车间生产的新产品更好,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011山东济南,27,9分)如图,矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线![]() 经过A、C两点,与AB边交于点D.
经过A、C两点,与AB边交于点D.
(1)求抛物线的函数表达式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式,并求出m为何值时,S取得最大值;
②当S最大时,在抛物线![]() 的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上,
上,![]() ,FD切
,FD切![]() 于点
于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,点
,点![]() 为
为![]() 中点,连接
中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
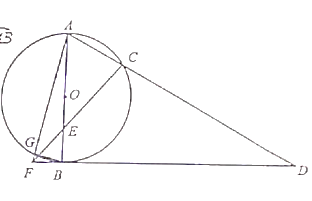
(1)求证:![]() ;
;
(2)若![]() 的半径为
的半径为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
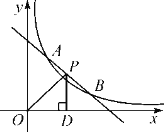
【题目】如图,一次函数y=-x+b与反比例函数y=![]() (x>0)的图象交于点A(m,3)和B(3,1).
(x>0)的图象交于点A(m,3)和B(3,1).
(1)求一次函数和反比例函数的解析式;
(2)点P(x,y)是直线AB上在第一象限内的一个点,过点P作PD⊥x轴于点D,连接OP,令△POD的面积为S,当S>![]() 时,直接写出点P横坐标x的取值范围.
时,直接写出点P横坐标x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com