
【题目】如图,等边三角形![]() 的边长为4厘米,长为1厘米的线段
的边长为4厘米,长为1厘米的线段![]() 在
在![]() 的边
的边![]() 上沿
上沿![]() 方向以1厘米/秒的速度向点
方向以1厘米/秒的速度向点![]() 运动(运动开始时,点
运动(运动开始时,点![]() 与点
与点![]() 重合,点
重合,点![]() 到达点
到达点![]() 时运动终止),过点
时运动终止),过点![]() 、
、![]() 分别作
分别作![]() 边的垂线,与
边的垂线,与![]() 的其他边交于
的其他边交于![]() 、
、![]() 两点.线段
两点.线段![]() 在运动的过程中,点
在运动的过程中,点![]() 、
、![]() 、
、![]() 、
、![]() 围成的图形的面积为
围成的图形的面积为![]() 平方厘米,运动的时间为
平方厘米,运动的时间为![]() 秒.则大致反映
秒.则大致反映![]() 与
与![]() 变化关系的图像是( )
变化关系的图像是( )

A.  .
. 
C. 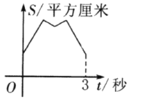 D.
D. 
【答案】A
【解析】
利用直角梯形的面积公式,由MN=1不变,可知四边形MNQP的面积随(PM+QN)的变化而变化,找到特殊点过点C作CG⊥AB,可分析得出四边形MNQP的面积变化情况.
解:过点C作CG⊥AB,
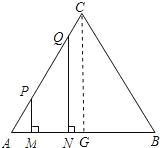
∵MN=1,四边形MNQP为直角梯形,
∴四边形MNQP的面积为S=![]() MN×(PM+QN),
MN×(PM+QN),
∴N点从A到G点四边形MNQP的面积为S=![]() MN×(PM+QN)中,PM,QN都在增大,所以面积也增大;
MN×(PM+QN)中,PM,QN都在增大,所以面积也增大;
当QN=CG时,QN开始减小,但PM仍然增大,且PM+QN不变,
∴四边形MNQP的面积不发生变化,
当PM<CG时,PM+QN开始减小,
∴四边形MNQP的面积减小,
∴符合要求的只有A.
故选:A.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料:
在学习“可化为一元一次方程的分式方程及其解法”的过程中,老师提出一个问题:若关于x的分式方程![]() =1的解为正数,求a的取值范围.
=1的解为正数,求a的取值范围.
经过独立思考与分析后,小杰和小哲开始交流解题思路如下:
小杰说:解这个关于x的分式方程,得x=a+4.由题意可得a+4>0,所以a>﹣4,问题解决.
小哲说:你考虑的不全面,还必须保证x≠4,即a+4≠4才行.
(1)请回答: 的说法是正确的,并简述正确的理由是 ;
(2)参考对上述问题的讨论,解决下面的问题:
若关于x的方程![]() 的解为非负数,求m的取值范围.
的解为非负数,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农庄计划在30亩空地上全部种植蔬菜和水果,菜农小张和果农小李分别承包了种植蔬菜和水果的任务.小张种植每亩蔬菜的工资y(元)与种植面积m(亩)之间的函数如图①所示,小李种植水果所得报酬z(元)与种植面积n(亩)之间函数关系如图②所示. 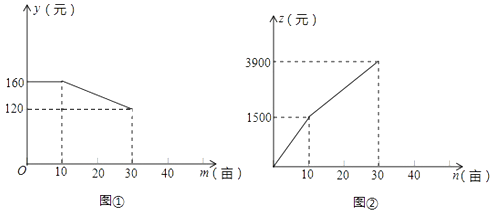
(1)如果种植蔬菜20亩,则小张种植每亩蔬菜的工资是元,小张应得的工资总额是元,此时,小李种植水果亩,小李应得的报酬是元;
(2)当10<n≤30时,求z与n之间的函数关系式;
(3)设农庄支付给小张和小李的总费用为w(元),当10<m≤30时,求w与m之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是第一象限内横坐标为2 ![]() 的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是 .
的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是 . 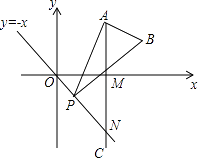
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AB=2BC,现给出下列结论:①sinA= ![]() ;②cosB=
;②cosB= ![]() ;③tanA=
;③tanA= ![]() ;④tanB=
;④tanB= ![]() ,其中正确的结论是(只需填上正确结论的序号)
,其中正确的结论是(只需填上正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某公司有三个住宅区可看作一点,A,B,C各区分别住有职工30人、15人、10人,且这三个住宅区在一条大道上(A,B,C三点共线),已知AB=100米,BC=200米.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
![]()
A. 点A B. 点B
C. A,B之间 D. B,C之间
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平安加气站某日8:00的储气量为10 000立方米.从8:00开始,3把加气枪同时以每车20立方米的加气量,依次给在加气站排队等候的若干辆车加气.8:30时,为缓解排队压力,又增开了2把加气枪.假设加气过程中每把加气枪加气的速度是匀速的,在不关闭加气枪的情况下,加气站的储气量![]() (立方米)与时间
(立方米)与时间![]() (小时)之间的函数关系如图中的折线
(小时)之间的函数关系如图中的折线![]() 所示.
所示.
(1)分别求出8:00 ~8:30及8:30之后加气站的储气量![]() (立方米)与时间
(立方米)与时间![]() (小时)之间的函数表达式.
(小时)之间的函数表达式.
(2)前30辆车能否在当天8:42之前加完气?
(3)若前![]() 辆车按上述方式加气,它们加完气的时间要比不增开加气枪加完气的时间提前1个小时,求
辆车按上述方式加气,它们加完气的时间要比不增开加气枪加完气的时间提前1个小时,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com