
【题目】阅读下列材料:
在学习“可化为一元一次方程的分式方程及其解法”的过程中,老师提出一个问题:若关于x的分式方程![]() =1的解为正数,求a的取值范围.
=1的解为正数,求a的取值范围.
经过独立思考与分析后,小杰和小哲开始交流解题思路如下:
小杰说:解这个关于x的分式方程,得x=a+4.由题意可得a+4>0,所以a>﹣4,问题解决.
小哲说:你考虑的不全面,还必须保证x≠4,即a+4≠4才行.
(1)请回答: 的说法是正确的,并简述正确的理由是 ;
(2)参考对上述问题的讨论,解决下面的问题:
若关于x的方程![]() 的解为非负数,求m的取值范围.
的解为非负数,求m的取值范围.
科目:初中数学 来源: 题型:
【题目】如图,将一块三角板和半圆形量角器按图中方式叠放,三角板一边与量角器的零刻度线所在直线重合,重叠部分的量角器弧( ![]() )对应的圆心角(∠AOB)为120°,OC的长为2cm,则三角板和量角器重叠部分的面积为 .
)对应的圆心角(∠AOB)为120°,OC的长为2cm,则三角板和量角器重叠部分的面积为 . 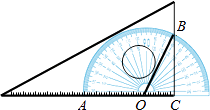
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y= ![]() x2+bx与直线y=2x交于点O(0,0),A(a,12).点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E.
x2+bx与直线y=2x交于点O(0,0),A(a,12).点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E.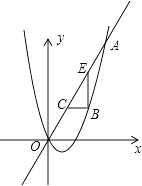
(1)求抛物线的函数解析式;
(2)若点C为OA的中点,求BC的长;
(3)以BC,BE为边构造矩形BCDE,设点D的坐标为(m,n),求出m,n之间的关系式.
(4)将射线OA绕原点旋转45°并与抛物线交于点P,求出P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
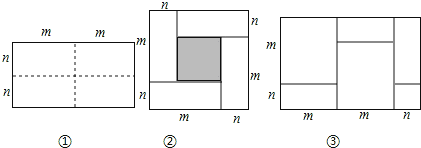
(1)按要求填空:
①你认为图②中的阴影部分的正方形的边长等于 ;
②请用两种不同的方法表示图②中阴影部分的面积:
方法1:
方法2:
③观察图②,请写出代数式(m+n)2,(m﹣n)2,mn这三个代数式之间的等量关系: ;
(2)根据(1)题中的等量关系,解决如下问题:若|m+n﹣6|+|mn﹣4|=0,求(m﹣n)2的值.
(3)实际上有许多代数恒等式可以用图形的面积来表示,如图③,它表示了 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,原有一大长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若原来该大长方形的周长是120,则分割后不用测量就能知道周长的图形标号为( )
A.①②
B.②③
C.①③
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一个“Z”型的工件(工件厚度忽略不计),如图示,其中AB为20cm,BC为60cm,∠ABC=90°,∠BCD=50°,求该工件如图摆放时的高度(即A到CD的距离).(结果精确到0.1m,参考数据:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y= ![]() (x﹣m)2﹣
(x﹣m)2﹣ ![]() m2+m的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.
m2+m的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.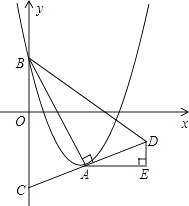
(1)当m=2时,求点B的坐标;
(2)求DE的长?
(3)①设点D的坐标为(x,y),求y关于x的函数关系式?②过点D作AB的平行线,与第(3)①题确定的函数图象的另一个交点为P,当m为何值时,以A,B,D,P为顶点的四边形是平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某公路(可视为![]() 轴)的同一侧有A、B、C三个村庄,要在公路边建一货栈D,向A、B、C三个村庄送农用物资,路线是D→A→B→C→D或D→C→B→A→D.试问在公路边是否存在一点D,使送货路线之和最短?若存在,请在图中画出点D所在的位置,简要说明作法;若不存在,请说明你的理由.
轴)的同一侧有A、B、C三个村庄,要在公路边建一货栈D,向A、B、C三个村庄送农用物资,路线是D→A→B→C→D或D→C→B→A→D.试问在公路边是否存在一点D,使送货路线之和最短?若存在,请在图中画出点D所在的位置,简要说明作法;若不存在,请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形![]() 的边长为4厘米,长为1厘米的线段
的边长为4厘米,长为1厘米的线段![]() 在
在![]() 的边
的边![]() 上沿
上沿![]() 方向以1厘米/秒的速度向点
方向以1厘米/秒的速度向点![]() 运动(运动开始时,点
运动(运动开始时,点![]() 与点
与点![]() 重合,点
重合,点![]() 到达点
到达点![]() 时运动终止),过点
时运动终止),过点![]() 、
、![]() 分别作
分别作![]() 边的垂线,与
边的垂线,与![]() 的其他边交于
的其他边交于![]() 、
、![]() 两点.线段
两点.线段![]() 在运动的过程中,点
在运动的过程中,点![]() 、
、![]() 、
、![]() 、
、![]() 围成的图形的面积为
围成的图形的面积为![]() 平方厘米,运动的时间为
平方厘米,运动的时间为![]() 秒.则大致反映
秒.则大致反映![]() 与
与![]() 变化关系的图像是( )
变化关系的图像是( )

A.  .
. 
C. 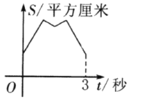 D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com