
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y= ![]() ��x��m��2��
��x��m��2�� ![]() m2+m�Ķ���ΪA����y��Ľ���ΪB������AB��AC��AB����y���ڵ�C���ӳ�CA����D��ʹAD=AC������BD����AE��x�ᣬDE��y�ᣮ
m2+m�Ķ���ΪA����y��Ľ���ΪB������AB��AC��AB����y���ڵ�C���ӳ�CA����D��ʹAD=AC������BD����AE��x�ᣬDE��y�ᣮ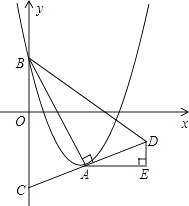
��1����m=2ʱ�����B�����ꣻ
��2����DE�ij���
��3�������D������Ϊ��x��y������y����x�ĺ�����ϵʽ���ڹ���D��AB��ƽ���ߣ���ڣ�3������ȷ���ĺ���ͼ�����һ������ΪP����mΪ��ֵʱ����A��B��D��PΪ������ı�����ƽ���ı��Σ�
���𰸡�
��1��
�⣺��m=2ʱ��y= ![]() ��x��2��2+1��
��x��2��2+1��
��x=0����y= ![]() ��x��2��2+1���ã�y=2��
��x��2��2+1���ã�y=2��
���B��������0��2��
��2��
�⣺�ӳ�EA����y���ڵ�F��
��AD=AC����AFC=��AED=90�㣬��CAF=��DAE��
���AFC�ա�AED��
��AF=AE��
�ߵ�A��m���� ![]() m2+m������B��0��m����
m2+m������B��0��m����
��AF=AE=|m|��BF=m������ ![]() m2+m��=
m2+m��= ![]() m2��
m2��
�ߡ�ABF=90�㩁��BAF=��DAE����AFB=��DEA=90�㣬
���ABF�ס�DAE��
�� ![]() ������
������ ![]() =
= ![]() ��
��
��DE=4��
��3��
�⣺�١ߵ�A������Ϊ��m���� ![]() m2+m����
m2+m����
���D��������2m���� ![]() m2+m+4����
m2+m+4����
��x=2m��y=�� ![]() m2+m+4��
m2+m+4��
��y=�� ![]()
![]() +
+ ![]() +4��
+4��
���������Ľ���ʽΪ��y=�� ![]() x2+
x2+ ![]() x+4��
x+4��
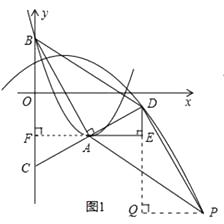
����PQ��DE�ڵ�Q�����DPQ�ա�BAF��
��i�����ı���ABDPΪƽ���ı���ʱ����ͼ1����
��P�ĺ�����Ϊ3m��
��P�������������� ![]() m2+m+4������
m2+m+4������ ![]() m2��=��
m2��=�� ![]() m2+m+4��
m2+m+4��
��P��3m���� ![]() m2+m+4�����������y=��
m2+m+4�����������y=�� ![]() x2+
x2+ ![]() x+4�ã�
x+4�ã�
�� ![]() m2+m+4=��
m2+m+4=�� ![]() ����3m��2+
����3m��2+ ![]() ����3m��+4��
����3m��+4��
��ã�m=0����ʱA��B��D��P��ͬһֱ���ϣ���ȥ����m=8��
��ii�����ı���ABPDΪƽ���ı���ʱ����ͼ2����
��P�ĺ�����Ϊm��
��P�������������� ![]() m2+m+4��+��
m2+m+4��+�� ![]() m2��=m+4��
m2��=m+4��
��P��m��m+4�����������y=�� ![]() x2+
x2+ ![]() x+4�ã�
x+4�ã�
m+4=�� ![]() m2+
m2+ ![]() m+4��
m+4��
��ã�m=0����ʱA��B��D��P��ͬһֱ���ϣ���ȥ����m=��8��
����������m��ֵΪ8��8��
����������1����m=2����ԭʽ���õ����κ����Ķ���ʽ���ݴ˼������B������ꣻ��2���ӳ�EA����y���ڵ�F��֤����AFC�ա�AED������֤����ABF�ס�DAE���������������ε����ʣ����DE=4����3���ٸ��ݵ�A�͵�B�����꣬�õ�x=2m��y=�� ![]() m2+m+4����m=
m2+m+4����m= ![]() ����y=��
����y=�� ![]() m2+m+4������������κ����ı���ʽ��
m2+m+4������������κ����ı���ʽ��
����PQ��DE�ڵ�Q�����DPQ�ա�BAF��Ȼ��֣���ͼ1���ͣ�ͼ2������������
�����㾫����������Ŀ����֪���������ö��κ��������ʵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ǵȱ������Σ���D��BC����һ���㣬��E��F�ֱ���AB��AC���ϣ�����AD��DE��DF���ҡ�ADE=��ADF=60�㣮
С��ͨ���۲졢ʵ�飬������룺�ڵ�D�˶��Ĺ����У�ʼ����AE=AF��С�������������ͬѧ�ǽ��н�����ͨ�����ۣ��γ���֤���ò���ļ����뷨��
�뷨1������AD�ǡ�EDF�Ľ�ƽ���ߣ������ADF��ȫ�������Σ�Ȼ��ͨ�����������ε����֪ʶ��֤��
�뷨2������AD�ǡ�EDF�Ľ�ƽ���ߣ������ƽ���ߵ����ʶ����Ļ���ͼ�Σ�Ȼ��ͨ��ȫ�������ε����֪ʶ��֤��
�뷨3������ACD�Ƶ�A˳ʱ����ת����ABG��ʹ��AC��AB�غϣ�Ȼ��ͨ��ȫ�������ε����֪ʶ��֤��
����ο�������뷨������С��֤��AE=AF����һ�ַ������ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�DZ߳�Ϊ6�ĵȱ������Σ�P��AC����һ���㣬��A��C�˶�����A��C���غϣ���Q��CB�ӳ�����һ���㣬���Pͬʱ����ͬ���ٶ���B��CB�ӳ��߷����˶���Q����B�غϣ�����P��PE��AB��E������PQ��AB��D��
��1����AE=1ʱ����AP�ij���
��2������BQD=30��ʱ����AP�ij���
��3�����˶��������߶�ED�ij��Ƿ����仯��������䣬����߶�ED�ij�����������仯����˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�
��ѧϰ���ɻ�ΪһԪһ�η��̵ķ�ʽ���̼���ⷨ���Ĺ����У���ʦ���һ�����⣺������x�ķ�ʽ����![]() =1�Ľ�Ϊ��������a��ȡֵ��Χ��
=1�Ľ�Ϊ��������a��ȡֵ��Χ��
��������˼���������С�ܺ�С�ܿ�ʼ��������˼·���£�
С��˵�����������x�ķ�ʽ���̣���x=a+4��������ɵ�a+4��0������a����4����������
С��˵���㿼�ǵIJ�ȫ�棬�����뱣֤x��4����a+4��4���У�
��1����ش��� ����˵������ȷ�ģ���������ȷ���������� ����
��2���ο���������������ۣ������������⣺
������x�ķ���![]() �Ľ�Ϊ�Ǹ�������m��ȡֵ��Χ��
�Ľ�Ϊ�Ǹ�������m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���B=90�㣬AB=6��BC=9������ABC�۵���ʹ��C��AB���е�D�غϣ��ۺ۽�AC�ڵ�M����BC�ڵ�N��
��1�����߶�BN�ij���
��2������CD����MN���ڵ�E��д�����E��ص�������ȷ���ۣ����� ����
���� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�У���CAB=��B=30�㣬AB=2 ![]() ����D��BC���ϣ��ѡ�ABC��AD����ʹAB��AC�غϣ��á�AB��D�����ABC���AB��D�ص����ֵ����Ϊ�� ��
����D��BC���ϣ��ѡ�ABC��AD����ʹAB��AC�غϣ��á�AB��D�����ABC���AB��D�ص����ֵ����Ϊ�� �� 
A.![]()
B.![]()
C.3�� ![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������BCO��������BAO����ij�ֱ任�õ��ģ�
(1)д��A��C�����ꣻ
(2)ͼ��A��C������֮��Ĺ�ϵ��ʲô��
(3)���������AOB������һ��M������Ϊ(x��y)����ô���Ķ�Ӧ��N��������ʲô��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijũׯ�ƻ���30Ķ�յ���ȫ����ֲ�߲˺�ˮ������ũС�ź�ũС��ֱ�а�����ֲ�߲˺�ˮ��������С����ֲÿĶ�߲˵Ĺ���y��Ԫ������ֲ���m��Ķ��֮��ĺ�����ͼ����ʾ��С����ֲˮ�����ñ���z��Ԫ������ֲ���n��Ķ��֮�亯����ϵ��ͼ����ʾ�� 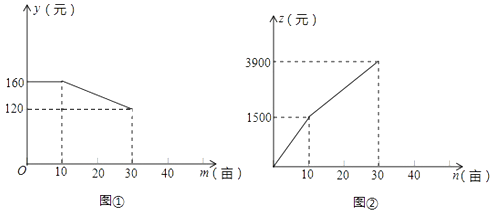
��1�������ֲ�߲�20Ķ����С����ֲÿĶ�߲˵Ĺ�����Ԫ��С��Ӧ�õĹ����ܶ���Ԫ����ʱ��С����ֲˮ��Ķ��С��Ӧ�õı�����Ԫ��
��2����10��n��30ʱ����z��n֮��ĺ�����ϵʽ��
��3����ũׯ֧����С�ź�С����ܷ���Ϊw��Ԫ������10��m��30ʱ����w��m֮��ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ܳ�Ϊ8�ġ�ABC��BC����ƽ��1����λ�õ���DEF�����ı���ABFD���ܳ�Ϊ�� �� 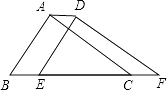
A.6
B.8
C.10
D.12
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com