
【题目】如图,将一块三角板和半圆形量角器按图中方式叠放,三角板一边与量角器的零刻度线所在直线重合,重叠部分的量角器弧( ![]() )对应的圆心角(∠AOB)为120°,OC的长为2cm,则三角板和量角器重叠部分的面积为 .
)对应的圆心角(∠AOB)为120°,OC的长为2cm,则三角板和量角器重叠部分的面积为 . 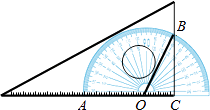
科目:初中数学 来源: 题型:
【题目】(2015随州)甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论:
①出发1小时时,甲、乙在途中相遇;
②出发1.5小时时,乙比甲多行驶了60千米;
③出发3小时时,甲、乙同时到达终点;
④甲的速度是乙速度的一半.
其中,正确结论的个数是( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在一条直线道路上分别从相距1500米的A,B 两点同时出发,相向而行,当两人相遇后,甲继续向点B前进(甲到达点B时停止运动),乙也立即向B点返回.在整个运动过程中,甲、乙均保持匀速运动.甲、乙两人之间的距离y(米)与乙运动的时间x(秒) 之间的关系如图所示.则甲到B点时,乙距B点的距离是________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据《2012年衢州市国民经济和社会发展统计公报》(2013年2月5日发布),衢州市固定资产投资的相关数据统计图如下: 
根据以上信息,解答下列问题:
(1)求2012年的固定资产投资增长速度(年增长速度即年增长率);
(2)求2005﹣2012年固定资产投资增长速度这组数据的中位数;
(3)求2006年的固定资产投资金额,并补全条形图;
(4)如果按照2012年的增长速度,请预测2013年衢州市的固定资产投资金额可达到多少亿元(精确到1亿元)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划从商店购买同一品牌的钢笔和文具盒,已知购买一个文具盒比购买一个钢笔多用20元,若用400元购买文具盒和用160元购买钢笔,则购买文具盒的个数是购买钢笔个数的一半.
(1)分别求出该品牌文具盒、钢笔的定价;
(2)经商谈,商店给予学校购买一个该品牌文具盒赠送一个该品牌钢笔的优惠,如果学校需要钢笔的个数是文具盒个数的2倍还多8个,且学校购买文具盒和钢笔的总费用不超过670元,那么该学校最多可购买多少个该品牌文具盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为( ) 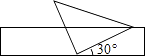
A.3cm
B.6cm
C.![]() cm
cm
D.![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,点D是BC边上一动点,点E,F分别在AB,AC边上,连接AD,DE,DF,且∠ADE=∠ADF=60°.
小明通过观察、实验,提出猜想:在点D运动的过程中,始终有AE=AF,小明把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:利用AD是∠EDF的角平分线,构造△ADF的全等三角形,然后通过等腰三角形的相关知识获证.
想法2:利用AD是∠EDF的角平分线,构造角平分线的性质定理的基本图形,然后通过全等三角形的相关知识获证.
想法3:将△ACD绕点A顺时针旋转至△ABG,使得AC和AB重合,然后通过全等三角形的相关知识获证.
请你参考上面的想法,帮助小明证明AE=AF.(一种方法即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD与四边形AEFG都是菱形,其中点C在AF上,点E,G分别在BC,CD上,若∠BAD=135°,∠EAG=75°,则 ![]() = .
= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
在学习“可化为一元一次方程的分式方程及其解法”的过程中,老师提出一个问题:若关于x的分式方程![]() =1的解为正数,求a的取值范围.
=1的解为正数,求a的取值范围.
经过独立思考与分析后,小杰和小哲开始交流解题思路如下:
小杰说:解这个关于x的分式方程,得x=a+4.由题意可得a+4>0,所以a>﹣4,问题解决.
小哲说:你考虑的不全面,还必须保证x≠4,即a+4≠4才行.
(1)请回答: 的说法是正确的,并简述正确的理由是 ;
(2)参考对上述问题的讨论,解决下面的问题:
若关于x的方程![]() 的解为非负数,求m的取值范围.
的解为非负数,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com