
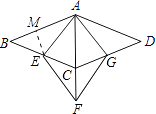
【题目】如图,四边形ABCD与四边形AEFG都是菱形,其中点C在AF上,点E,G分别在BC,CD上,若∠BAD=135°,∠EAG=75°,则 ![]() = .
= . 
【答案】![]()
【解析】解:∵∠BAD=135°,∠EAG=75°,四边形ABCD与四边形AEFG都是菱形, ∴∠B=180°﹣∠BAD=45°,∠BAE=∠BAC﹣∠EAC=30°,
过点E作EM⊥AB于点M,设EM=x,
在Rt△AEM中,AE=2EM=2x,AM= ![]() x,
x,
在Rt△BEM中,BM=x,
则 ![]() =
= ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】本题主要考查了等腰直角三角形和含30度角的直角三角形的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,第1次平移将矩形ABCD沿AB的方向向右平移5个单位,得到矩形A1B1C1D1 , 第2次平移将矩形A1B1C1D1沿A1B1的方向向右平移5个单位,得到矩形A2B2C2D2…,第n次平移将矩形An﹣1Bn﹣1Cn﹣1Dn﹣1沿An﹣1Bn﹣1的方向平移5个单位,得到矩形AnBnCnDn(n>2). 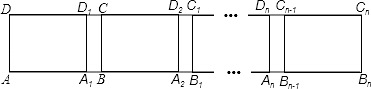
(1)求AB1和AB2的长.
(2)若ABn的长为56,求n.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一块三角板和半圆形量角器按图中方式叠放,三角板一边与量角器的零刻度线所在直线重合,重叠部分的量角器弧( ![]() )对应的圆心角(∠AOB)为120°,OC的长为2cm,则三角板和量角器重叠部分的面积为 .
)对应的圆心角(∠AOB)为120°,OC的长为2cm,则三角板和量角器重叠部分的面积为 . 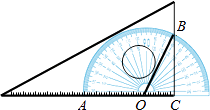
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年5月7日浙江省11个城市的空气质量指数(AQI)如图所示: 
(1)这11个城市当天的空气质量指数的极差、众数和中位数分别是多少?
(2)当0≤AQI≤50时,空气质量为优.求这11个城市当天的空气质量为优的频率;
(3)求宁波、嘉兴、舟山、绍兴、台州五个城市当天的空气质量指数的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一点A从数轴上表示+2的点开始移动,第一次先向左移动1个单位,再向右移动2个单位;第二次先向左移动3个单位,再向右移动4个单位;第三次先向左移动5个单位,再向右移动6个单位……
(1)写出第一次移动后这个点在数轴上表示的数为 ;
(2)写出第二次移动后这个点在数轴上表示的数为 ;
(3)写出第五次移动后这个点在数轴上表示的数为 ;
(4)写出第![]() 次移动结果这个点在数轴上表示的数为 ;
次移动结果这个点在数轴上表示的数为 ;
(5)如果第![]() 次移动后这个点在数轴上表示的数为56,求
次移动后这个点在数轴上表示的数为56,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况,部分数据如表:
温度t/℃ | ﹣4 | ﹣2 | 0 | 1 | 4 |
植物高度增长量l/mm | 41 | 49 | 49 | 46 | 25 |
科学家经过猜想、推测出l与t之间是二次函数关系.由此可以推测最适合这种植物生长的温度为℃.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y= ![]() x2+bx与直线y=2x交于点O(0,0),A(a,12).点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E.
x2+bx与直线y=2x交于点O(0,0),A(a,12).点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E.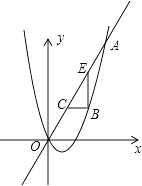
(1)求抛物线的函数解析式;
(2)若点C为OA的中点,求BC的长;
(3)以BC,BE为边构造矩形BCDE,设点D的坐标为(m,n),求出m,n之间的关系式.
(4)将射线OA绕原点旋转45°并与抛物线交于点P,求出P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
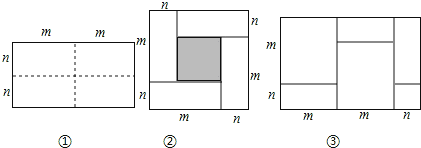
(1)按要求填空:
①你认为图②中的阴影部分的正方形的边长等于 ;
②请用两种不同的方法表示图②中阴影部分的面积:
方法1:
方法2:
③观察图②,请写出代数式(m+n)2,(m﹣n)2,mn这三个代数式之间的等量关系: ;
(2)根据(1)题中的等量关系,解决如下问题:若|m+n﹣6|+|mn﹣4|=0,求(m﹣n)2的值.
(3)实际上有许多代数恒等式可以用图形的面积来表示,如图③,它表示了 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某公路(可视为![]() 轴)的同一侧有A、B、C三个村庄,要在公路边建一货栈D,向A、B、C三个村庄送农用物资,路线是D→A→B→C→D或D→C→B→A→D.试问在公路边是否存在一点D,使送货路线之和最短?若存在,请在图中画出点D所在的位置,简要说明作法;若不存在,请说明你的理由.
轴)的同一侧有A、B、C三个村庄,要在公路边建一货栈D,向A、B、C三个村庄送农用物资,路线是D→A→B→C→D或D→C→B→A→D.试问在公路边是否存在一点D,使送货路线之和最短?若存在,请在图中画出点D所在的位置,简要说明作法;若不存在,请说明你的理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com