
【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
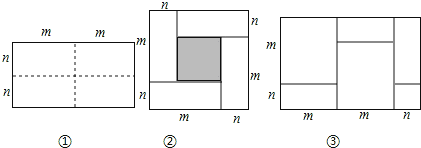
(1)按要求填空:
①你认为图②中的阴影部分的正方形的边长等于 ;
②请用两种不同的方法表示图②中阴影部分的面积:
方法1:
方法2:
③观察图②,请写出代数式(m+n)2,(m﹣n)2,mn这三个代数式之间的等量关系: ;
(2)根据(1)题中的等量关系,解决如下问题:若|m+n﹣6|+|mn﹣4|=0,求(m﹣n)2的值.
(3)实际上有许多代数恒等式可以用图形的面积来表示,如图③,它表示了 .
【答案】(1)①m﹣n;②(m﹣n)2;(m+n)2﹣4mn,③(m﹣n)2=(m+n)2﹣4mn;(2)(m﹣n)2=20;(3)(2m+n)(m+n)=2m2+3mn+n2
【解析】
(1)①观察可得阴影部分的正方形边长是m-n;
②方法1:阴影部分的面积就等于边长为m-n的小正方形的面积;方法2:边长为m+n的大正方形的面积减去4个长为m,宽为n的长方形面积;
③根据以上相同图形的面积相等可得;
(2)根据|m+n-6|+|mn-4|=0可得m+n=6、mn=4,利用(1)中结论(m-n)2=(m+n)2-4mn计算可得;
(3)根据:大长方形面积等于长乘以宽或两个边长分别为m、n的正方形加上3个长为m、宽为n的小长方形面积和列式可得.
(1)①阴影部分的正方形边长是m﹣n.
②方法1:阴影部分的面积就等于边长为m﹣n的小正方形的面积,
即(m﹣n)2,
方法2:边长为m+n的大正方形的面积减去4个长为m,宽为n的长方形面积,即(m+n)2﹣4mn;
③(m﹣n)2=(m+n)2﹣4mn.
(2))∵|m+n﹣6|+|mn﹣4|=0,
∴m+n﹣6=0,mn﹣4=0,
∴m+n=6,mn=4
∵由(1)可得(m﹣n)2=(m+n)2﹣4mn
∴(m﹣n)2=(m+n)2﹣4mn=62﹣4×4=20,
∴(m﹣n)2=20;
(3)根据大长方形面积等于长乘以宽有:(2m+n)(m+n),
或两个边长分别为m、n的正方形加上3个长为m、宽为n的小长方形面积和有:2m2+3mn+n2,
故可得:(2m+n)(m+n)=2m2+3mn+n2.
故答案为:(1)m﹣n;(2)①(m﹣n)2,②(m+n)2﹣4mn,③(m﹣n)2=(m+n)2﹣4mn;(3)(2m+n)(m+n)=2m2+3mn+n2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】据《2012年衢州市国民经济和社会发展统计公报》(2013年2月5日发布),衢州市固定资产投资的相关数据统计图如下: 
根据以上信息,解答下列问题:
(1)求2012年的固定资产投资增长速度(年增长速度即年增长率);
(2)求2005﹣2012年固定资产投资增长速度这组数据的中位数;
(3)求2006年的固定资产投资金额,并补全条形图;
(4)如果按照2012年的增长速度,请预测2013年衢州市的固定资产投资金额可达到多少亿元(精确到1亿元)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD与四边形AEFG都是菱形,其中点C在AF上,点E,G分别在BC,CD上,若∠BAD=135°,∠EAG=75°,则 ![]() = .
= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图。 
(1)问题 如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.求证: ![]() .
.
(2)探究 如图,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.
(3)应用 请利用(1)(2)获得的经验解决问题
如图3,在△ABD中,AB=6,AD=BD=5,点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠CPD=∠A.设点P的运动时间为t(秒),当以D为圆心,DC为半径的圆与AB相切时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)若AE=1时,求AP的长;
(2)当∠BQD=30°时,求AP的长;
(3)在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果发生变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片ABCD对折后再展开,得到折痕EF,M是BC上一点,沿着AM再次折叠纸片,使得点B恰好落在折痕EF上的点B′处,连接AB′、BB′.

判断△AB′B的形状为 ;
若P为线段EF上一动点,当PB+PM最小时,请描述点P的位置为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
在学习“可化为一元一次方程的分式方程及其解法”的过程中,老师提出一个问题:若关于x的分式方程![]() =1的解为正数,求a的取值范围.
=1的解为正数,求a的取值范围.
经过独立思考与分析后,小杰和小哲开始交流解题思路如下:
小杰说:解这个关于x的分式方程,得x=a+4.由题意可得a+4>0,所以a>﹣4,问题解决.
小哲说:你考虑的不全面,还必须保证x≠4,即a+4≠4才行.
(1)请回答: 的说法是正确的,并简述正确的理由是 ;
(2)参考对上述问题的讨论,解决下面的问题:
若关于x的方程![]() 的解为非负数,求m的取值范围.
的解为非负数,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠CAB=∠B=30°,AB=2 ![]() ,点D在BC边上,把△ABC沿AD翻折使AB与AC重合,得△AB′D,则△ABC与△AB′D重叠部分的面积为( )
,点D在BC边上,把△ABC沿AD翻折使AB与AC重合,得△AB′D,则△ABC与△AB′D重叠部分的面积为( ) 
A.![]()
B.![]()
C.3﹣ ![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是第一象限内横坐标为2 ![]() 的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是 .
的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是 . 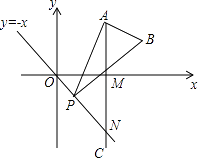
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com