
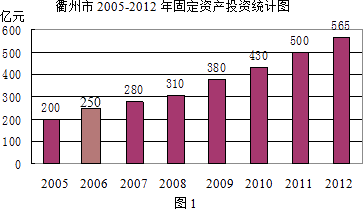
【题目】据《2012年衢州市国民经济和社会发展统计公报》(2013年2月5日发布),衢州市固定资产投资的相关数据统计图如下: 
根据以上信息,解答下列问题:
(1)求2012年的固定资产投资增长速度(年增长速度即年增长率);
(2)求2005﹣2012年固定资产投资增长速度这组数据的中位数;
(3)求2006年的固定资产投资金额,并补全条形图;
(4)如果按照2012年的增长速度,请预测2013年衢州市的固定资产投资金额可达到多少亿元(精确到1亿元)?
【答案】
(1)解:根据题意得出:
![]() ×100%=13%;
×100%=13%;
答:2012年的固定资产投资增长速度为13%
(2)解:数据按大小排列得出:
10.71%,12%,13%,13.16%,16.28%,18.23%,22.58,25%,
∴中位数为: ![]() =14.72%;
=14.72%;
答:2005﹣2012年固定资产投资增长速度这组数据的中位数是14.72%
(3)解:设2006年的固定资产投资金额为x亿元,则有:
280﹣x=12%x(或x﹣200=25%×200),
解得:x=250,
答:2006年的投资额是250亿元;
如图所示;
(4)解:565×(1+13%)=638.45≈638(亿元),
答:预测2013年可达638亿元
【解析】(1)根据2012年和2011年投资进而求出增长率即可;(2)根据中位数的定义,按大小排列后找出最中间的两个求出平均数即可;(3)设2006年的固定资产投资金额为x亿元,进而得出280﹣x=12%x求出即可;(4)根据2012年的增长率,得出565×(1+13%)求出即可.
【考点精析】解答此题的关键在于理解条形统计图的相关知识,掌握能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况,以及对折线统计图的理解,了解能清楚地反映事物的变化情况,但是不能清楚地表示出在总体中所占的百分比.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某校举办八年级学生数学素养大赛,比赛共设四个项目:七巧板拼图,趣题巧解,数学应用,魔方复原,每个项目得分都按一定百分比折算后记入总分,下表为甲,乙,丙三位同学得分情况(单位:分)
七巧板拼图 | 趣题巧解 | 数学应用 | 魔方复原 | |
甲 | 66 | 89 | 86 | 68 |
乙 | 66 | 60 | 80 | 68 |
丙 | 66 | 80 | 90 | 68 |
(1)比赛后,甲猜测七巧板拼图,趣题巧解,数学应用,魔方复原这四个项目得分分别按10%,40%,20%,30%折算记入总分,根据猜测,求出甲的总分;
(2)本次大赛组委会最后决定,总分为80分以上(包含80分)的学生获一等奖,现获悉乙,丙的总分分别是70分,80分.甲的七巧板拼图、魔方复原两项得分折算后的分数和是20分,问甲能否获得这次比赛的一等奖?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,第1次平移将矩形ABCD沿AB的方向向右平移5个单位,得到矩形A1B1C1D1 , 第2次平移将矩形A1B1C1D1沿A1B1的方向向右平移5个单位,得到矩形A2B2C2D2…,第n次平移将矩形An﹣1Bn﹣1Cn﹣1Dn﹣1沿An﹣1Bn﹣1的方向平移5个单位,得到矩形AnBnCnDn(n>2). 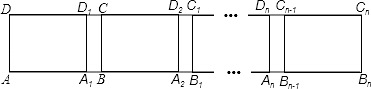
(1)求AB1和AB2的长.
(2)若ABn的长为56,求n.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 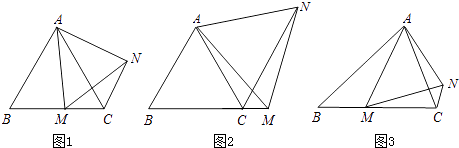
(1)【提出问题】
如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
(2)【类比探究】
如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
(3)【拓展延伸】
如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y1=﹣x+4的图象与函数y2= ![]() (x>0)的图象交于A(a,1)、B(1,b)两点.
(x>0)的图象交于A(a,1)、B(1,b)两点. 
(1)求函数y2的表达式;
(2)观察图象,比较当x>0时,y1与y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一块三角板和半圆形量角器按图中方式叠放,三角板一边与量角器的零刻度线所在直线重合,重叠部分的量角器弧( ![]() )对应的圆心角(∠AOB)为120°,OC的长为2cm,则三角板和量角器重叠部分的面积为 .
)对应的圆心角(∠AOB)为120°,OC的长为2cm,则三角板和量角器重叠部分的面积为 . 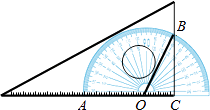
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年5月7日浙江省11个城市的空气质量指数(AQI)如图所示: 
(1)这11个城市当天的空气质量指数的极差、众数和中位数分别是多少?
(2)当0≤AQI≤50时,空气质量为优.求这11个城市当天的空气质量为优的频率;
(3)求宁波、嘉兴、舟山、绍兴、台州五个城市当天的空气质量指数的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
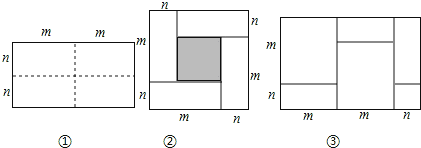
(1)按要求填空:
①你认为图②中的阴影部分的正方形的边长等于 ;
②请用两种不同的方法表示图②中阴影部分的面积:
方法1:
方法2:
③观察图②,请写出代数式(m+n)2,(m﹣n)2,mn这三个代数式之间的等量关系: ;
(2)根据(1)题中的等量关系,解决如下问题:若|m+n﹣6|+|mn﹣4|=0,求(m﹣n)2的值.
(3)实际上有许多代数恒等式可以用图形的面积来表示,如图③,它表示了 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com