
����Ŀ�� 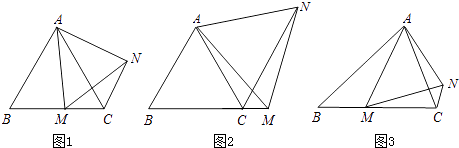
��1����������⡿
��ͼ1���ڵȱߡ�ABC�У���M��BC�ϵ�����һ�㣨�����˵�B��C��������AM����AMΪ�����ȱߡ�AMN������CN����֤����ABC=��ACN��
��2�������̽����
��ͼ2���ڵȱߡ�ABC�У���M��BC�ӳ����ϵ�����һ�㣨�����˵�C���������������䣬��1���н��ۡ�ABC=��ACN����������˵�����ɣ�
��3������չ���졿
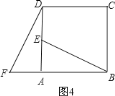
��ͼ3���ڵ�����ABC�У�BA=BC����M��BC�ϵ�����һ�㣨�����˵�B��C��������AM����AMΪ����������AMN��ʹ���ǡ�AMN=��ABC������CN����̽����ABC���ACN��������ϵ����˵�����ɣ�
���𰸡�
��1��֤�����ߡ�ABC����AMN�ǵȱ������Σ�
��AB=AC��AM=AN����BAC=��MAN=60�㣬
���BAM=��CAN��
���ڡ�BAM�͡�CAN�У�
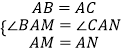
���BAM�ա�CAN��SAS����
���ABC=��ACN
��2���⣺���ۡ�ABC=��ACN�Գ�����
�������£��ߡ�ABC����AMN�ǵȱ������Σ�
��AB=AC��AM=AN����BAC=��MAN=60�㣬
���BAM=��CAN��
���ڡ�BAM�͡�CAN�У�
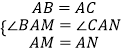
���BAM�ա�CAN��SAS����
���ABC=��ACN
��3���⣺��ABC=��ACN��
�������£���BA=BC��MA=MN�����ǡ�ABC=��AMN��
��ǡ�BAC=��MAN��
���ABC�ס�AMN��
�� ![]() ��
��
�֡ߡ�BAM=��BAC����MAC����CAN=��MAN����MAC��
���BAM=��CAN��
���BAM�ס�CAN��
���ABC=��ACN
����������1������SAS��֤����BAM�ա�CAN���̶��ó����ۣ���2��Ҳ����ͨ��֤����BAM�ա�CAN���ó����ۣ��ͣ�1����˼·��ȫһ������3�����ȵó���BAC=��MAN���Ӷ��ж���ABC�ס�AMN���õ� ![]() �����ݡ�BAM=��BAC����MAC����CAN=��MAN����MAC���õ���BAM=��CAN���Ӷ��ж���BAM�ס�CAN���ó����ۣ�
�����ݡ�BAM=��BAC����MAC����CAN=��MAN����MAC���õ���BAM=��CAN���Ӷ��ж���BAM�ס�CAN���ó����ۣ�
�����㾫����������Ҫ�����˵ȱ������ε����ʺ����������ε��ж������ʵ����֪ʶ�㣬��Ҫ���յȱ������ε������Ƕ���Ȳ���ÿ���Ƕ���60�㣻���������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ��������ȷ�����⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��Rt��ABC�У���ABC=90�㣬ADƽ�֡�BAC��BC��D�� 
��1���ó߹滭ԲO��ʹԲO��A��D���㣬��Բ��O�ڱ�AC�ϣ���������ͼ�ۼ�����д������
��2����֤��BC��ԲO���У�
��3����ԲO��AB�ڵ�E����AE=2��CD=2BD�����߶�BE�ij��ͻ�DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ּ��У����ϵȳ���13���������ӹ̸ּܣ���AP1=P1P2=P2P3=��=P13P14=P14A�����A�Ķ����� �� 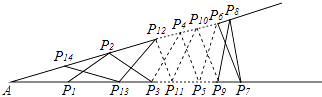
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������һ��ֱ�ߵ�·�Ϸֱ�����1500��A��B ����ͬʱ������������У������������������Bǰ���������Bʱֹͣ�˶�������Ҳ������B�㷵�أ��������˶������У��ס��Ҿ����������˶����ס�������֮��ľ���y���ף������˶���ʱ��x���룩 ֮��Ĺ�ϵ��ͼ��ʾ�����B��ʱ���Ҿ�B��ľ�����________�ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�
��ͼ![]() ����
����![]() ��ֱ��
��ֱ��![]() ƽ���ƶ��߶�
ƽ���ƶ��߶�![]() �ij��ȣ����Ա䵽
�ij��ȣ����Ա䵽![]() ��λ�ã�
��λ�ã�
��ͼ![]() ����
����![]() Ϊ�ᣬ��
Ϊ�ᣬ��![]() ����
����![]() �����Ա䵽
�����Ա䵽![]() ��λ�ã�
��λ�ã�
��ͼ![]() ���Ե�
���Ե�![]() Ϊ���ģ���
Ϊ���ģ���![]() ��ת
��ת![]() �����Ա䵽
�����Ա䵽![]() ��λ�ã�
��λ�ã�
������������һ��������������һ�������ΰ�ƽ���ƶ������ۡ���ת�ȷ�����ɵģ�����ֻ�ı�λ�ã����ı���״��С��ͼ�α任�����������ε�ȫ�ȱ任��
�ش��������⣺
����ͼ![]() �У�����ͨ��ƽ���ƶ������ۡ���ת�е���һ�ַ��������仯��ʹ
�У�����ͨ��ƽ���ƶ������ۡ���ת�е���һ�ַ��������仯��ʹ![]() �䵽
�䵽![]() ��λ�ã�
��λ�ã�
��ָͼ���߶�![]() ��
��![]() ֮��Ĺ�ϵ��Ϊʲô��
֮��Ĺ�ϵ��Ϊʲô��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ݡ�2012�������й��ú���ᷢչͳ�ƹ�������2013��2��5�շ������������й̶��ʲ�Ͷ�ʵ��������ͳ��ͼ���£� 
����������Ϣ������������⣺
��1����2012��Ĺ̶��ʲ�Ͷ�������ٶȣ��������ٶȼ��������ʣ���
��2����2005��2012��̶��ʲ�Ͷ�������ٶ��������ݵ���λ����
��3����2006��Ĺ̶��ʲ�Ͷ�ʽ�����ȫ����ͼ��
��4���������2012��������ٶȣ���Ԥ��2013�������еĹ̶��ʲ�Ͷ�ʽ��ɴﵽ������Ԫ����ȷ��1��Ԫ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ�ƻ����̵깺��ͬһƷ�Ƶĸֱʺ��ľߺУ���֪����һ���ľߺбȹ���һ���ֱʶ���20Ԫ������400Ԫ�����ľߺк���160Ԫ����ֱʣ������ľߺеĸ����ǹ���ֱʸ�����һ�룮
��1���ֱ������Ʒ���ľߺС��ֱʵĶ��ۣ�
��2������̸���̵����ѧУ����һ����Ʒ���ľߺ�����һ����Ʒ�Ƹֱʵ��Żݣ����ѧУ��Ҫ�ֱʵĸ������ľߺи�����2������8������ѧУ�����ľߺкֱʵ��ܷ��ò�����670Ԫ����ô��ѧУ���ɹ�����ٸ���Ʒ���ľߺУ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ǵȱ������Σ���D��BC����һ���㣬��E��F�ֱ���AB��AC���ϣ�����AD��DE��DF���ҡ�ADE=��ADF=60�㣮
С��ͨ���۲졢ʵ�飬������룺�ڵ�D�˶��Ĺ����У�ʼ����AE=AF��С�������������ͬѧ�ǽ��н�����ͨ�����ۣ��γ���֤���ò���ļ����뷨��
�뷨1������AD�ǡ�EDF�Ľ�ƽ���ߣ������ADF��ȫ�������Σ�Ȼ��ͨ�����������ε����֪ʶ��֤��
�뷨2������AD�ǡ�EDF�Ľ�ƽ���ߣ������ƽ���ߵ����ʶ����Ļ���ͼ�Σ�Ȼ��ͨ��ȫ�������ε����֪ʶ��֤��
�뷨3������ACD�Ƶ�A˳ʱ����ת����ABG��ʹ��AC��AB�غϣ�Ȼ��ͨ��ȫ�������ε����֪ʶ��֤��
����ο�������뷨������С��֤��AE=AF����һ�ַ������ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�DZ߳�Ϊ6�ĵȱ������Σ�P��AC����һ���㣬��A��C�˶�����A��C���غϣ���Q��CB�ӳ�����һ���㣬���Pͬʱ����ͬ���ٶ���B��CB�ӳ��߷����˶���Q����B�غϣ�����P��PE��AB��E������PQ��AB��D��
��1����AE=1ʱ����AP�ij���
��2������BQD=30��ʱ����AP�ij���
��3�����˶��������߶�ED�ij��Ƿ����仯��������䣬����߶�ED�ij�����������仯����˵������.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com