
【题目】细观察,找规律 下列各图中的MA1与NAn平行.
(1)图①中的∠A1+∠A2=度, 图②中的∠A1+∠A2+∠A3=度,
图③中的∠A1+∠A2+∠A3+∠A4=度,
图④中的∠A1+∠A2+∠A3+∠A4+∠A5=度,
…,
第⑩个图中的∠A1+∠A2+∠A3+…+∠A11=度
(2)第n个图中的∠A1+∠A2+∠A3+…+∠An+1=
(3)请你证明图②的结论.
【答案】
(1)180;360;540;720;1800
(2)180n°
(3)证明:过A2作BA2平行MA1,如图所示.
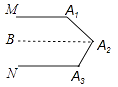
∵M A1∥NA3,
∴BA2∥NA3,
∴∠A1+∠BA2 A1=180°,∠BA2 A3+∠A3=180°,
∴∠A1+∠A2+∠A 3=∠A1+∠BA2 A1 +∠BA2 A3+∠A3=360°.
【解析】解:(1)图①中的∠A1+∠A2=180°, 图②中的∠A1+∠A2+∠A3=180°×2=360°,
图③中的∠A1+∠A2+∠A3+∠A4=180°×3=540°,
图④中的∠A1+∠A2+∠A3+∠A4+∠A5=180°×4=720°,
…,
第⑩个图中的∠A1+∠A2+∠A3+…+∠A11=180°×10=1800°,
所以答案是:180;360;540;720;1800.(2)根据(1)即可得出:第n个图中的∠A1+∠A2+∠A3+…+∠An+1=180n°.
所以答案是:180n°.
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.


科目:初中数学 来源: 题型:
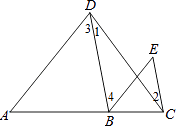
【题目】按图填空,并注明理由. 已知:如图,∠1=∠2,∠3=∠E.
求证:AD∥BE.
证明:∵∠1=∠2 (已知)
∴∥
()
∴∠E=∠
()
又∵∠E=∠3 ( 已知 )
∴∠3=∠
()
∴AD∥BE.
()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知圆的半径为r,圆心到直线a的距离为d,d和r分别是方程x2﹣7x+10=0的两根,则直线a与圆的位置关系是( )
A. 相交B. 相切C. 相交或相离D. 相离
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点F是BC的中点,点E是线段AB的延长线上的一动点,连接EF,过点C作AB的平行线CD,与线段EF的延长线交于点D,连接CE、BD. 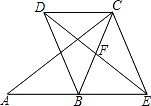
(1)求证:四边形DBEC是平行四边形.
(2)若∠ABC=120°,AB=BC=4,则在点E的运动过程中: ①当BE=时,四边形BECD是矩形,试说明理由;
②当BE=时,四边形BECD是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com