
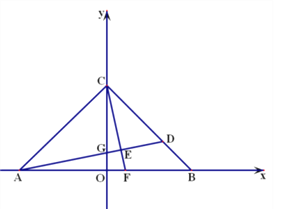
【题目】如图,在平面直角坐标系中,OA=OB=OC=6,过点A的直线AD交BC于点D,交y轴与点G,△ABD的面积为△ABC面积的![]() .
.
(1)直接写出点D的坐标;
(2)过点C作CE⊥AD,交AB交于F,垂足为E.
①求证:OF=OG;(3分) ②求点F的坐标.
(3)在(2)的条件下,在第一象限内是否存在点P,使△CFP为等腰直角三角形,若存在,直接写出点P坐标;若不存在,请说明理由.
【答案】(1) D(4,2);(2) ①证明见解析; ②F(1.2,0); (3)存在,∴P(6,7.2),(7.2,1.2),(3.6,3.6).
【解析】分析:(1)作DH⊥AB于H,由OA=OB=OC=6,就可以得出∠ABC=45°,由三角形的面积公式就可以求出DH的值,就可以求出BH的值,从而求出D的坐标; (2)①根据OA=OC,再根据直角三角形的性质就可以得出△AOG≌△COF,就可以得出OF=OG;②由△AOG∽△AHD就可以得出OG的值,就可以求出F的坐标.(3)根据条件作出图形图1,作PH⊥OC于H,PM⊥OB于M,由△PHC≌△PMF就可以得出结论,图2,作PH⊥OB于H,由△COF≌△PHF就可以得出结论,图3,作PH⊥OC于H,由△COF≌△PHC就可以得出结论.
本题解析:
(1)作DH⊥AB于H,∴∠AHD=∠BHD=90°.∵OA=OB=OC=6,∴AB=12,
∴S△ABC=![]() =36,∵△ABD的面积为△ABC面积的
=36,∵△ABD的面积为△ABC面积的![]() .∴
.∴![]() ×36=
×36=![]() ,∴DH=2.
,∴DH=2.
∵OC=OB,∴∠BCO=∠OBC.∵∠BOC=90°,∴∠BCO=∠OBC=45°,∴∠HDB=45°,∴∠HDB=∠DBH,
∴DH=BH.∴BH=2.∴OH=4,∴D(4,2);
(2)①∵CE⊥AD,∴∠CEG=∠AEF=90°,∵∠AOC=∠COF=90°,∴∠COF=∠AEF=90°
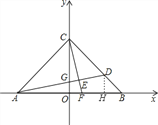
∴∠AFC+∠FAG=90°,∠AFC+∠OCF=90°,∴∠FAG=∠OCF.
在△AOG和△COF中
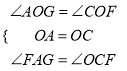 ,
,
∴△AOG≌△COF(ASA),∴OF=OG;
②∵∠AOG=∠AHD=90°,∴OG∥DH,∴△AOG∽△AHD,
∴![]() ,∴
,∴![]() ,∴OG=1.2.∴OF=1.2.∴F(1.2,0)
,∴OG=1.2.∴OF=1.2.∴F(1.2,0)
(3)如图1,当∠CPF=90°,PC=PF时,作PH⊥OC于H,PM⊥OB于M
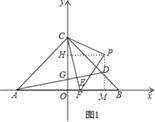
∴∠PHC=∠PHO=∠PMO=∠PMB=90°.∵∠BOC=90°,∴四边形OMPH是矩形,
∴∠HPM=90°,∴∠HPF+∠MPF=90°.∵∠CPF=90°,∴∠CPH+∠HPF=90°.
∵∠CPH=∠FPM.
在△PHC和△PMF中
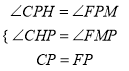 ,
,
∴△PHC≌△PMF(AAS),∴CH=FM.HP=PM,∴矩形HPMO是正方形,∴HO=MO=HP=PM.
∵CO=OB,∴COOH=OBOM,∴CH=MB,∴FM=MB.∵OF=1.2,∴FB=4.8,∴FM=2.4,
∴OM=3.6∴PM=3.6,∴P(3.6,3.6);
图2,当∠CFP=90,PF=CF时,作PH⊥OB于H,
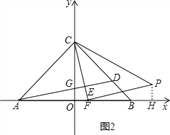
∴∠OFC+∠PFH=90,∠PHF=90,∴∠PFH+∠FPH=90,∴∠OFC=∠HPF.
∵∠COF=90,∴∠COF=∠FHP.
在△COF和△PHF中
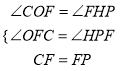 ,
,
∴△COF≌△PHF(AAS),∴OF=HP,CO=FH,∴HP=1.2,FH=6,∴OH=7.2,∴P(7.2,1.2);
图3,当∠FCP=90,PC=CF时,作PH⊥OC于H,
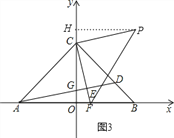
∴∠CHP=90,∴∠HCP+∠HPC=90.∵∠FCP=90,∴∠HCP+∠OCF=90,
∴∠OCF=∠HCP.∵∠FOC=90,∴∠FOC=∠CHP.
在△COF和△PHC中
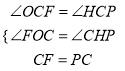 ,
,
∴△COF≌△PHC(AAS),∴OF=HC,OC=HP,∴HC=1.2,HP=6,∴HO=7.2,∴P(6,7.2),
∴P(6,7.2),(7.2,1.2),(3.6,3.6).


科目:初中数学 来源: 题型:
【题目】先阅读下列的解答过程,然后作答:
形如![]() 的化简,只要我们找到两个数a、b使a+b=m,ab=n,这样(
的化简,只要我们找到两个数a、b使a+b=m,ab=n,这样(![]() )2+(
)2+(![]() )2=m
)2=m![]() ·
·![]() =n,那么便有
=n,那么便有![]() =
=![]() =
=![]() ±
±![]() (a>b) .例如:化简
(a>b) .例如:化简![]() 解:首先把
解:首先把![]() 化为
化为![]() ,这里m=7,n=12;由于4+3=7,4×3=12,即(
,这里m=7,n=12;由于4+3=7,4×3=12,即(![]() )2+(
)2+(![]() )2=7
)2=7![]() ·
·![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() =2+
=2+![]() .
.
由上述例题的方法化简:(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 已知∠ABC=90°,点P为射线BC上任意一点(点P与点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连接QE并延长交BP于点F. 试说明:(1)△ABP≌△AEQ;(2)EF=BF
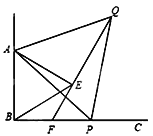
查看答案和解析>>
科目:初中数学 来源: 题型:
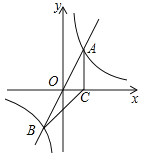
【题目】(2016四川省乐山市第24题)如图,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
(1)求k的值;
(2)x轴上是否存在一点D,使△ABD为直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:
①该抛物线的对称轴在y轴左侧;
②关于x的方程ax2+bx+c+2=0无实数根;
③a﹣b+c≥0;
④![]() 的最小值为3.
的最小值为3.
其中,正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com