
【题目】已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:
①该抛物线的对称轴在y轴左侧;
②关于x的方程ax2+bx+c+2=0无实数根;
③a﹣b+c≥0;
④![]() 的最小值为3.
的最小值为3.
其中,正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
科目:初中数学 来源: 题型:
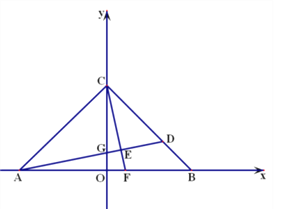
【题目】如图,在平面直角坐标系中,OA=OB=OC=6,过点A的直线AD交BC于点D,交y轴与点G,△ABD的面积为△ABC面积的![]() .
.
(1)直接写出点D的坐标;
(2)过点C作CE⊥AD,交AB交于F,垂足为E.
①求证:OF=OG;(3分) ②求点F的坐标.
(3)在(2)的条件下,在第一象限内是否存在点P,使△CFP为等腰直角三角形,若存在,直接写出点P坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
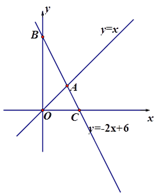
【题目】如图,直线![]() 与x轴、
与x轴、![]() 轴分别相交于点C、B,与直线
轴分别相交于点C、B,与直线![]() 相交于
相交于
点A.
(1)点B、点C和点A的坐标分别是(0, )、( ,0)、( , );
(2)求两条直线与![]() 轴围成的三角形的面积;
轴围成的三角形的面积;
(3)在坐标轴上是否存在一点Q,使△OAQ的面积等于6,若存在请直接写出Q点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:
①abc>0
②4a+2b+c>0
③4ac﹣b2<8a
④![]() <a<
<a<![]()
⑤b>c.
其中含所有正确结论的选项是( )

A.①③ B.①③④ C.②④⑤ D.①③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com