
【题目】如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
【答案】
(1)解:补全图形,如图所示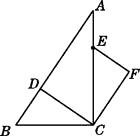
(2)证明:由旋转的性质得:∠DCF=90°,DC=FC,BC=EC,∴∠DCE+∠ECF=90°
∵∠ACB=90°,
∴∠DCE+∠BCD=90°.
∴∠ECF=∠BCD.
∵EF∥DC,
∴∠EFC+∠DCF=180°.
∴∠EFC=90°,
在△BDC和△EFC中,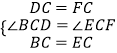
∴△BDC≌△EFC(SAS).
∴∠BDC=∠EFC=90°
【解析】(1)根据题意将线段CD绕点C按顺时针方向旋转90°,画出图形即可。
(2)根据旋转的性质得出∠DCF=90°,DC=FC,BC=EC,∠DCE+∠ECF=90°,再证明∠ECF=∠BCD,∠EFC=90°,然后证明△BDC≌△EFC,再根据全等三角形的性质即可证得结论。


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】在全运会射击比赛的选拔赛中,运动员甲10次射击成绩的统计表(表1)和扇形统计图如下: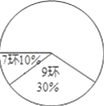
命中环数 | 10 | 9 | 8 | 7 |
命中次数 | 3 | 2 |
(1)根据统计表(图)中提供的信息,补全统计表及扇形统计图;
(2)已知乙运动员10次射击的平均成绩为9环,方差为1.2,如果只能选一人参加比赛,你认为应该派谁去?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC
(1)①用直尺和圆规作出∠ACB的角平分线CD;(不写作法,但保留作图痕迹)
②过点D画出△ADC的高DE和△DCB的高DF;
(2)量出DE,DF的长度,你有怎样的发现?并把你的发现用文字语言表达出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DABC中,AB=BC=AC=12cm,现有两点M,N分别从现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.
(1)点M、N运动几秒后,M、N两点重合?
(2)点M、N运动几秒后,可得到等边三角形△AMN?
(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形?如存在,请求出此时M、N运动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个书架上的方格中放着四本厚度和长度相同的书,其中左边两边上紧贴书架方格内侧竖放,右边两本书自然向左斜放,支撑点为C,E,右侧书角正好靠在方格内侧上,若书架方格长BF=40cm,∠DCE=30°.
(1)设一本书的厚度为acm,则EF= cm(结果保留根号);
(2)若书的长度AB=20cm,求一本书的厚度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.
(1)求证:四边形ABCD是矩形.
(2)若∠ADF:∠FDC=3:2,DF⊥AC,则∠BDF的度数是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com