
【题目】已知![]() 的周长为28,过点
的周长为28,过点![]() 分别作
分别作![]() ,交直线
,交直线![]() 于点
于点![]() ,
,![]() ,交直线
,交直线![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长为____.
的长为____.
【答案】![]() 或
或![]()
【解析】
根据∠A为锐角或∠D为锐角分情况进行讨论,由ABCD的周长为28,DE⊥BC,DF⊥AB,垂足分别为E、F,且DE=3,DF=4,构造方程求解即可求得答案.
对于平行四边形ABCD有两种情况:
当∠A为锐角时,如图1,
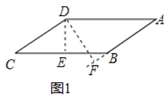
设BC=a,AB=b,
∵平行四边形ABCD,DE⊥AB,DF⊥BC,
∴AB×DE=BC×DF,AB=CD,BC=DA,
又∵DE=3,DF=4,
∴3a=4b,
∵平行四边形ABCD的周长为28,
∴2(a+b)=28,
∴a+b=14,
则 ,
,
解得:![]() ,
,
∴BC=8,AB=6,
∴AB=CD=6,AD=BC=8,
∴在Rt△CDE中,CE=3![]() ,
,
∴BE=BC-CE=8-3![]() ,
,
∴在Rt△ADF中,AF=4![]() ,
,
∵F点在AB的延长线上,
∴BF=AF-AB=4![]() -6,
-6,
∴BE+BF=(8-3![]() )+(4
)+(4![]() -6)=2+
-6)=2+![]() ;
;
当∠D为锐角时,如图2,
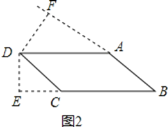
设BC=a,AB=b,
∵平行四边形ABCD,DE⊥BC,DF⊥AB,
∴AB×DF=BC×DE,AB=CD,BC=DA,
又∵DE=3,DF=4,
∴3a=4b,
∵平行四边形ABCD的周长为28,
∴2(a+b)=28,
∴a+b=14,
解方程组 ,
,
解得:![]() ,
,
∴BC=8,AB=6,
∴AB=CD=6,AD=BC=8,
∴在Rt△CDE中,CE=3![]() ,
,
∴BE=BC+CE=8+3![]() ,
,
∴在Rt△ADF中,AF=4![]() ,
,
∵F点在AB的延长线上,
∴BF=AF+AB=4![]() +6,
+6,
∴BE+BF=(8+3![]() )+(4
)+(4![]() +6)=14+7
+6)=14+7![]() ,
,
故答案为:2+![]() 或14+7
或14+7![]() .
.


科目:初中数学 来源: 题型:
【题目】对任意有理数x,用[x]表示不大于x的最大整数.例如:[1.3]=1,[3]=3,[﹣2.5]=﹣3.以下结论正确的是_____.(把你认为正确结论的序号都填上)
①[﹣3.14]=﹣4;
②﹣[﹣x]=[x];
③[2x]=2[x];
④若[![]() ]=﹣4,则x的取值范围是﹣
]=﹣4,则x的取值范围是﹣![]() ≤x<﹣
≤x<﹣![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一块矩形木板,木工采用如图的方式,在木板上截出两个面积分别为18dm2和32dm2的正方形木板.
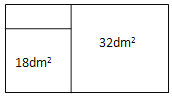
(1)求剩余木料的面积.
(2)如果木工想从剩余的木料中截出长为1.5dm,宽为ldm的长方形木条,最多能截出 块这样的木条.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,弧AE等于弧AB,BE分别交AD、AC于点F、G. 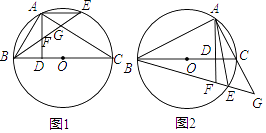
(1)判断△FAG的形状,并说明理由;
(2)若点E和点A在BC的两侧,BE、AC的延长线交于点G,AD的延长线交BE于点F,其余条件不变,(1)中的结论还成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1) 发现:
如图1,点![]() 是线段
是线段![]() 外一动点,且
外一动点,且![]() ,
,![]() .当点
.当点![]() 位于 时,线段
位于 时,线段![]() 的长取得最大值;最大值为 (用含
的长取得最大值;最大值为 (用含![]() ,
,![]() 的式子表示).
的式子表示).

(2)应用:
如图2,点![]() 为线段
为线段![]() 外一动点,
外一动点,![]() ,
,![]() ,分别以
,分别以![]() ,
,![]() 为边在
为边在![]() 外部作等边
外部作等边![]() 和等边
和等边![]() ,连接
,连接![]() ,
,![]() .
.
①求证:![]() ;
;
②直接写出线段![]() 长的最大值.
长的最大值.
(3)拓展:
如图3,在平面直角坐标系中,点![]() ,点
,点![]() ,点
,点![]() 为线段
为线段![]() 外一动点,
外一动点,![]() ,
,![]() ,
,![]() ,请直接写出线段
,请直接写出线段![]() 长的最大值及此时点
长的最大值及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数 ![]() 分别交y轴、x 轴于A、B两点,抛物线
分别交y轴、x 轴于A、B两点,抛物线 ![]() 过A、B两点.
过A、B两点.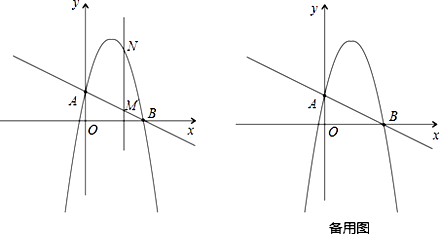
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于点M,交这个抛物线于点N.求当t 取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com