˝â´đŁş˝âŁşŁ¨1ŁŠĄ÷PQRľÄąßQRžšýľăBĘąŁŹĄ÷ABQššłÉľČŃüÖą˝ÇČý˝ÇĐÎŁŹ
ĄŕAB=AQŁŹź´3=4-tŁŹ
Ąŕt=1ŁŽ
ź´ľąt=1ĂëĘąŁŹĄ÷PQRľÄąßQRžšýľăBŁŽ
Ł¨2ŁŠ˘Ůľą0ĄÜtĄÜ1ĘąŁŹČç´đÍź1-1ËůĘžŁŽ
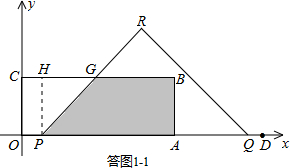
ÉčPR˝ťBCÓÚľăGŁŹ
šýľăP×÷PHĄÍBCÓÚľăHŁŹÔňCH=OP=2tŁŹGH=PH=3ŁŽ
S=S
žŘĐÎOABC-S
ĚÝĐÎOPGC=8ĄÁ3-
Ł¨2t+2t+3ŁŠĄÁ3
=
-6tŁť
˘Úľą1ŁźtĄÜ2ĘąŁŹČç´đÍź1-2ËůĘžŁŽ
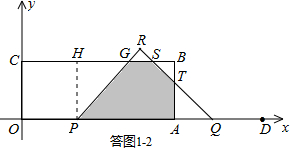
ÉčPR˝ťBCÓÚľăGŁŹRQ˝ťBCĄ˘ABÓÚľăSĄ˘TŁŽ
šýľăP×÷PHĄÍBCÓÚľăHŁŹÔňCH=OP=2tŁŹGH=PH=3ŁŽ
QD=tŁŹÔňAQ=AT=4-tŁŹ
ĄŕBT=BS=AB-AQ=3-Ł¨4-tŁŠ=t-1ŁŽ
S=S
žŘĐÎOABC-S
ĚÝĐÎOPGC-S
Ą÷BST=8ĄÁ3-
Ł¨2t+2t+3ŁŠĄÁ3-
Ł¨t-1ŁŠ
2=-
t
2-5t+19Łť
˘Űľą2ŁźtĄÜ4ĘąŁŹČç´đÍź1-3ËůĘžŁŽ
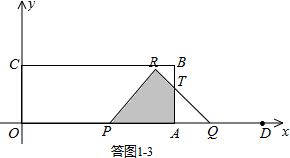
ÉčRQÓëAB˝ťÓÚľăTŁŹÔňAT=AQ=4-tŁŽ
PQ=12-3tŁŹĄŕPR=RQ=
Ł¨12-3tŁŠŁŽ
S=S
Ą÷PQR-S
Ą÷AQT=
PR
2-
AQ
2=
Ł¨12-3tŁŠ
2-
Ł¨4-tŁŠ
2=
t
2-14t+28ŁŽ
×ŰÉĎËůĘöŁŹSšŘÓÚtľÄşŻĘýšŘϾʽΪŁş
S=
| | -6t(0ĄÜtĄÜ1) | | -t2-5t+19(1ŁźtĄÜ2) | | t2-14t+28(2ŁźtĄÜ4) |
| |
ŁŽ
Ł¨3ŁŠĄßEŁ¨5ŁŹ0ŁŠŁŹĄŕAE=AB=3ŁŹ
ĄŕËÄąßĐÎABFEĘÇŐýˇ˝ĐÎŁŽ
Čç´đÍź2ŁŹ˝ŤĄ÷AMEČĆľăA˳ʹŐëĐýת90ĄăŁŹľĂľ˝Ą÷ABMĄäŁŹĆäÖĐAEÓëABÖغϣŽ
ĄßĄĎMAN=45ĄăŁŹ
ĄŕĄĎEAM+ĄĎNAB=45ĄăŁŹ
ĄŕĄĎBAMĄä+ĄĎNAB=45ĄăŁŹ
ĄŕĄĎMAN=ĄĎMĄäANŁŽ
ÁŹ˝ÓMNŁŽÔÚĄ÷MANÓëĄ÷MĄäANÖĐŁŹ
| | AM=AMĄä | | ĄĎMAN=ĄĎMĄäAN | | AN=AN |
| |
ĄŕĄ÷MANĄŐĄ÷MĄäANŁ¨SASŁŠŁŽ
ĄŕMN=MĄäN=MĄäB+BN
ĄŕMN=EM+BNŁŽ
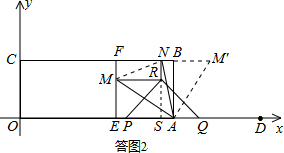
ÉčEM=mŁŹBN=nŁŹÔňFM=3-mŁŹFN=3-nŁŽ
ÔÚRtĄ÷FMNÖĐŁŹÓÉš´šÉś¨ŔíľĂŁşFM
2+FN
2=MN
2ŁŹź´Ł¨3-mŁŠ
2+Ł¨3-nŁŠ
2=Ł¨m+nŁŠ
2ŁŹ
ŐűŔíľĂŁşmn+3Ł¨m+nŁŠ-9=0ŁŽ ˘Ů
ŃÓł¤NR˝ťxÖáÓÚľăSŁŹÔňm=EM=RS=
PQ=
Ł¨12-3tŁŠŁŹ
ĄßQS=
PQ=
Ł¨12-3tŁŠŁŹAQ=4-tŁŹ
Ąŕn=BN=AS=QS-AQ=
Ł¨12-3tŁŠ-Ł¨4-tŁŠ=2-
tŁŽ
Ąŕm=3nŁŹ
´úČë˘ŮĘ˝ŁŹťŻźňľĂŁşn
2+4n-3=0ŁŹ
˝âľĂn=-2+
ťňn=-2-
Ł¨ÉáČĽŁŠ
Ąŕ2-
t=-2+
˝âľĂŁşt=8-2
ŁŽ
ĄŕČôĄĎMAN=45ĄăŁŹÔňtľÄ־ΪŁ¨8-2
ŁŠĂ룎

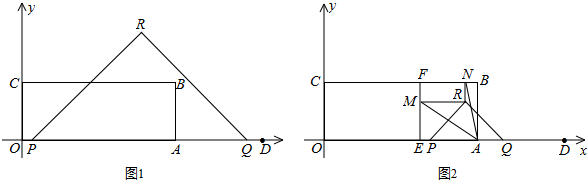






 ÓŔÇŹ˝ĚÓýşŽźŮ×÷ŇľżěŔÖźŮĆÚŃÓąßČËĂńłö°ćÉçĎľÁĐ´đ°¸
ÓŔÇŹ˝ĚÓýşŽźŮ×÷ŇľżěŔÖźŮĆÚŃÓąßČËĂńłö°ćÉçĎľÁĐ´đ°¸
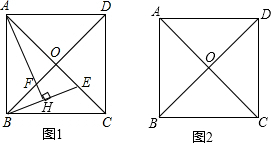 ČçÍźŁŹŇŃÖŞŐýˇ˝ĐÎABCDŁŹACĄ˘BDĎཝÓÚľăOŁŹEÎŞACÉĎŇťľăŁŹAHĄÍEB˝ťEBÓÚľăHŁŹAH˝ťBDÓÚľăFŁŽ
ČçÍźŁŹŇŃÖŞŐýˇ˝ĐÎABCDŁŹACĄ˘BDĎཝÓÚľăOŁŹEÎŞACÉĎŇťľăŁŹAHĄÍEB˝ťEBÓÚľăHŁŹAH˝ťBDÓÚľăFŁŽ ČçÍźŁŹÖąĎßy=kx-2ÓëxÖὝÓÚľăAŁ¨1ŁŹ0ŁŠŁŹÓëyÖὝÓÚľăBŁŹČôÖąĎßABÉϾľăCÔÚľÚČýĎóĎŢŁŹÇŇSĄ÷BOC=3ŁŹÇóľăCľÄ×řąęŁŽ
ČçÍźŁŹÖąĎßy=kx-2ÓëxÖὝÓÚľăAŁ¨1ŁŹ0ŁŠŁŹÓëyÖὝÓÚľăBŁŹČôÖąĎßABÉϾľăCÔÚľÚČýĎóĎŢŁŹÇŇSĄ÷BOC=3ŁŹÇóľăCľÄ×řąęŁŽ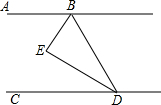 ČçÍźŁŹŇŃÖŞŁŹBEĆ˝ˇÖĄĎABDŁŹDEĆ˝ˇÖĄĎBDCŁŹÇŇĄĎEBD+ĄĎEDB=90ĄăŁŽ
ČçÍźŁŹŇŃÖŞŁŹBEĆ˝ˇÖĄĎABDŁŹDEĆ˝ˇÖĄĎBDCŁŹÇŇĄĎEBD+ĄĎEDB=90ĄăŁŽ