
【题目】![]() 问题解决:
问题解决:![]() 如图1,在平面直角坐标系xOy中,一次函数
如图1,在平面直角坐标系xOy中,一次函数![]() 与x轴交于点A,与y轴交于点B,以AB为腰在第二象限作等腰直角
与x轴交于点A,与y轴交于点B,以AB为腰在第二象限作等腰直角![]() ,
,![]() ,点A、B的坐标分别为A______、B______.
,点A、B的坐标分别为A______、B______.
![]() 求
求![]() 中点C的坐标.小明同学为了解决这个问题,提出了以下想法:过点C向x轴作垂线交x轴于点
中点C的坐标.小明同学为了解决这个问题,提出了以下想法:过点C向x轴作垂线交x轴于点![]() 请你借助小明的思路,求出点C的坐标;
请你借助小明的思路,求出点C的坐标;
![]() 类比探究:数学老师表扬了小明同学的方法,然后提出了一个新的问题,如图2,在平面直角坐标系xOy中,点A坐标
类比探究:数学老师表扬了小明同学的方法,然后提出了一个新的问题,如图2,在平面直角坐标系xOy中,点A坐标![]() ,点B坐标
,点B坐标![]() ,过点B作x轴垂线l,点P是l上一动点,点D是在一次函数
,过点B作x轴垂线l,点P是l上一动点,点D是在一次函数![]() 图象上一动点,若
图象上一动点,若![]() 是以点D为直角顶点的等腰直角三角形,请直接写出点D与点P的坐标.
是以点D为直角顶点的等腰直角三角形,请直接写出点D与点P的坐标.

【答案】(1)①![]()
![]() ,②
,②![]() ;(2)
;(2)![]() ,
,![]() 或
或![]() ,
,![]() .
.
【解析】
(1)利用坐标轴上点的特点建立方程求解,即可得出结论;
(2)先构造出△AEC≌△BOA,求出AE,CE,即可得出结论;
(3)同(2)的方法构造出△AFD≌△DGP(AAS),分两种情况,建立方程求解即可得出结论.
解:![]() 针对于一次函数
针对于一次函数![]() ,
,
令![]() ,
,
![]() ,
,
![]() ,
,
令![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
故答案为![]() ,
,![]() ;
;
![]() 如图1
如图1

由![]() 知,
知,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
过点C作![]() 轴于E,
轴于E,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,
在![]() 和
和![]() 中,
中, ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ;
;
![]() 如图2,
如图2,![]() 过点D作
过点D作![]() 轴于F,延长FD交BP于G,
轴于F,延长FD交BP于G,
![]() ,
,
![]() 点D在直线
点D在直线![]() 上,
上,
![]() 设点
设点![]() ,
,
![]() ,
,
![]() 轴,
轴,![]() ,
,
![]() ,
,
同![]() 的方法得,
的方法得,![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
如图2,![]() ,
,
![]() ,
,
![]() ,
,
![]() 或
或![]() ,
,
![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
即:![]() ,
,![]() 或
或![]() ,
,![]()
![]() 利用坐标轴上点的特点建立方程求解,即可得出结论;
利用坐标轴上点的特点建立方程求解,即可得出结论;
![]() 先构造出
先构造出![]() ≌
≌![]() ,求出AE,CE,即可得出结论;
,求出AE,CE,即可得出结论;
![]() 同
同![]() 的方法构造出
的方法构造出![]() ≌
≌![]() ,分两种情况,建立方程求解即可得出结论.
,分两种情况,建立方程求解即可得出结论.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】(3分)以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( )

A. 如图1,展开后测得∠1=∠2
B. 如图2,展开后测得∠1=∠2且∠3=∠4
C. 如图3,测得∠1=∠2
D. 如图4,展开后再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD
查看答案和解析>>
科目:初中数学 来源: 题型:
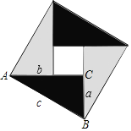
【题目】现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°,若AC=b,BC=a,请你利用这个图形解决下列问题:
(1)试说明a2+b2=c2;
(2)如果大正方形的面积是6,小正方形的面积是2,求(a+b)2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,矩形 ABCO,B点坐标为(4,3),抛物线y=![]() 经过矩形ABCO的顶点 B 、C ,D为BC的中点,直线 AD y轴交 E点,与抛物线
经过矩形ABCO的顶点 B 、C ,D为BC的中点,直线 AD y轴交 E点,与抛物线 ![]() 交于第四象限的 F点.
交于第四象限的 F点.
(1)求该抛物线解析式与F点坐标;
(2)如图2,动点P从点C出发,沿线段 CB以每秒1个单位长度的速度向终点B运动;同时,动点M从 A出发,沿线 AE以每秒 ![]() 个单位长度的速度向终点E运动.过点P作PH ⊥OA,垂足为H ,连接 MP ,MH .设点 P 的运动时间 t秒.
个单位长度的速度向终点E运动.过点P作PH ⊥OA,垂足为H ,连接 MP ,MH .设点 P 的运动时间 t秒.
①问EP+ PH+ HF是否有最小值?如果有,求出t的值;如果没有,请说明理由.
②若△PMH是等腰三角形,请直接写出此时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点坐标为A(-2.3)、B(-6,0)、C(-1,0)
(1) 将△ABC绕坐标原点O旋转180°,画出图形,并写出点A的对应点A′ 的坐标________;
(2)将△ABC绕坐标原点O逆时针旋转90°,
直接写出点A的对应点A″的坐标___________;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空
如图:∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F,求证:CE∥DF.请完成下面的解题过程.

解:∵BD平分∠ABC,CE平分∠ACB ( 已知 )
∴∠DBC=![]() ∠_____,∠ECB=
∠_____,∠ECB=![]() ∠_____ ( 角平分线的定义)
∠_____ ( 角平分线的定义)
又∵∠ABC=∠ACB (已知)
∴∠_____=∠_____.
又∵∠_____=∠_____ (已知)
∴∠F=∠_____
∴CE∥DF_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,BD是斜边上高动点P从点A出发沿AB边由A向终点B以
,BD是斜边上高动点P从点A出发沿AB边由A向终点B以![]() 的速度匀速移动,动点Q从点B出发沿射线BC以
的速度匀速移动,动点Q从点B出发沿射线BC以![]() 的速度匀速移动,点P、Q同时出发,当点P停止运动,点Q也随之停止
的速度匀速移动,点P、Q同时出发,当点P停止运动,点Q也随之停止![]() 连接AQ,交射线BD于点
连接AQ,交射线BD于点![]() 设点P运动时间为t秒.
设点P运动时间为t秒.
![]() 在运动过程中,
在运动过程中,![]() 的面积始终是
的面积始终是![]() 的面积的2倍,为什么?
的面积的2倍,为什么?
![]() 当点Q在线段BC上运动时,t为何值时,
当点Q在线段BC上运动时,t为何值时,![]() 和
和![]() 相等.
相等.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com