
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,BD是斜边上高动点P从点A出发沿AB边由A向终点B以
,BD是斜边上高动点P从点A出发沿AB边由A向终点B以![]() 的速度匀速移动,动点Q从点B出发沿射线BC以
的速度匀速移动,动点Q从点B出发沿射线BC以![]() 的速度匀速移动,点P、Q同时出发,当点P停止运动,点Q也随之停止
的速度匀速移动,点P、Q同时出发,当点P停止运动,点Q也随之停止![]() 连接AQ,交射线BD于点
连接AQ,交射线BD于点![]() 设点P运动时间为t秒.
设点P运动时间为t秒.
![]() 在运动过程中,
在运动过程中,![]() 的面积始终是
的面积始终是![]() 的面积的2倍,为什么?
的面积的2倍,为什么?
![]() 当点Q在线段BC上运动时,t为何值时,
当点Q在线段BC上运动时,t为何值时,![]() 和
和![]() 相等.
相等.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】![]() 问题解决:
问题解决:![]() 如图1,在平面直角坐标系xOy中,一次函数
如图1,在平面直角坐标系xOy中,一次函数![]() 与x轴交于点A,与y轴交于点B,以AB为腰在第二象限作等腰直角
与x轴交于点A,与y轴交于点B,以AB为腰在第二象限作等腰直角![]() ,
,![]() ,点A、B的坐标分别为A______、B______.
,点A、B的坐标分别为A______、B______.
![]() 求
求![]() 中点C的坐标.小明同学为了解决这个问题,提出了以下想法:过点C向x轴作垂线交x轴于点
中点C的坐标.小明同学为了解决这个问题,提出了以下想法:过点C向x轴作垂线交x轴于点![]() 请你借助小明的思路,求出点C的坐标;
请你借助小明的思路,求出点C的坐标;
![]() 类比探究:数学老师表扬了小明同学的方法,然后提出了一个新的问题,如图2,在平面直角坐标系xOy中,点A坐标
类比探究:数学老师表扬了小明同学的方法,然后提出了一个新的问题,如图2,在平面直角坐标系xOy中,点A坐标![]() ,点B坐标
,点B坐标![]() ,过点B作x轴垂线l,点P是l上一动点,点D是在一次函数
,过点B作x轴垂线l,点P是l上一动点,点D是在一次函数![]() 图象上一动点,若
图象上一动点,若![]() 是以点D为直角顶点的等腰直角三角形,请直接写出点D与点P的坐标.
是以点D为直角顶点的等腰直角三角形,请直接写出点D与点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明:
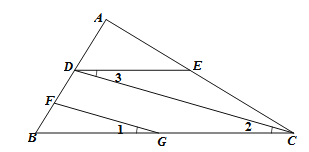
如图,FG//CD,∠1=∠3,∠B=50°,求∠BDE的度数.
解:∵FG//CD (已知)
∴∠2=_________( )
又∵∠1=∠3
∴∠3=∠_________( )
∴BC//__________( )
∴∠B+________=180°( )
又∵∠B=50°
∴∠BDE=130°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天早晨,小玲从家出发匀速步行到学校,小玲出发一段时间后,她的妈妈发现小玲忘带了一件必需的学习用品,于是立即下楼骑自行车,沿小玲行进的路线,匀速去追小玲,妈妈追上小玲将学习用品交给小玲后,立即沿原路线匀速返回家里,但由于路上行人渐多,妈妈返回时骑车的速度只是原来速度的一半,小玲继续以原速度步行前往学校,妈妈与小玲之间的距离y(米)与小玲从家出发后步行的时间x(分)之间的关系如图所示(小玲和妈妈上、下楼以及妈妈交学习用品给小玲耽搁的时间忽略不计).当妈妈刚回到家时,小玲离学校的距离为_____米.
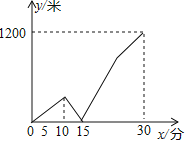
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB分别与⊙O相切于点A、B,点M在PB上,且OM∥AP,MN⊥AP,垂足为N.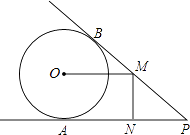
(1)求证:OM=AN;
(2)若⊙O的半径R=3,PA=9,求OM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,![]() ,
,![]() ,
,![]() .
.
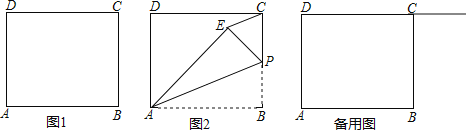
![]() 为边BC上一点,将
为边BC上一点,将![]() 沿直线AP翻折至
沿直线AP翻折至![]() 的位置
的位置![]() 点B落在点E处
点B落在点E处![]()
![]() 如图1,当点E落在CD边上时,利用尺规作图,在图1中作出满足条件的图形
如图1,当点E落在CD边上时,利用尺规作图,在图1中作出满足条件的图形![]() 不写作法,保留作图痕迹,用2B铅笔加粗加黑
不写作法,保留作图痕迹,用2B铅笔加粗加黑![]() 并直接写出此时
并直接写出此时![]() ______;
______;
![]() 如图2,若点P为BC边的中点,连接CE,则CE与AP有何位置关系?请说明理由;
如图2,若点P为BC边的中点,连接CE,则CE与AP有何位置关系?请说明理由;
![]() 点Q为射线DC上的一个动点,将
点Q为射线DC上的一个动点,将![]() 沿AQ翻折,点D恰好落在直线BQ上的点
沿AQ翻折,点D恰好落在直线BQ上的点![]() 处,则
处,则![]() ______;
______;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有A. B.C三点,分别表示有理数26,10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设点P移动时间为t秒。
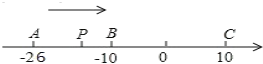
(1)PA= ,PC= (用含t的代数式表示)
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,当点P运动到点C时,P、Q两点运动停止,
①当P、Q两点运动停止时,求点P和点Q的距离;
②求当t为何值时P、Q两点恰好在途中相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程组解应用题某校组织“大手拉小手,义卖献爱心”活动,计划购买黑、白两种颜色的文化衫进行手绘设计后出售,并将所获利润全部捐给山区困难孩子.已知该学校从批发市场花2400元购买了黑、白两种颜色的文化衫100件,每件文化衫的批发价及手绘后的零售价如表:
批发价(元) | 零售价(元) | |
黑色文化衫 | 25 | 45 |
白色文化衫 | 20 | 35 |
(1)学校购进黑、白文化衫各几件?
(2)通过手绘设计后全部售出,求该校这次义卖活动所获利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
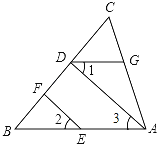
【题目】填空,完成下列证明过程,并在括号中注明理由.
如图,已知∠CGD=∠CAB,∠1=∠2,求证:∠ADF+∠CFE=180°
证明:∵∠CGD=∠CAB
∴DG∥______(______)
∴∠1=______(______)
∵∠1=∠2
∴∠2=∠3(______)
∴EF∥______(______)
∴∠ADF+∠CFE=180°(______)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com