
【题目】填空,完成下列证明过程,并在括号中注明理由.
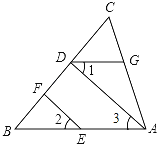
如图,已知∠CGD=∠CAB,∠1=∠2,求证:∠ADF+∠CFE=180°
证明:∵∠CGD=∠CAB
∴DG∥______(______)
∴∠1=______(______)
∵∠1=∠2
∴∠2=∠3(______)
∴EF∥______(______)
∴∠ADF+∠CFE=180°(______)
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,BD是斜边上高动点P从点A出发沿AB边由A向终点B以
,BD是斜边上高动点P从点A出发沿AB边由A向终点B以![]() 的速度匀速移动,动点Q从点B出发沿射线BC以
的速度匀速移动,动点Q从点B出发沿射线BC以![]() 的速度匀速移动,点P、Q同时出发,当点P停止运动,点Q也随之停止
的速度匀速移动,点P、Q同时出发,当点P停止运动,点Q也随之停止![]() 连接AQ,交射线BD于点
连接AQ,交射线BD于点![]() 设点P运动时间为t秒.
设点P运动时间为t秒.
![]() 在运动过程中,
在运动过程中,![]() 的面积始终是
的面积始终是![]() 的面积的2倍,为什么?
的面积的2倍,为什么?
![]() 当点Q在线段BC上运动时,t为何值时,
当点Q在线段BC上运动时,t为何值时,![]() 和
和![]() 相等.
相等.

查看答案和解析>>
科目:初中数学 来源: 题型:
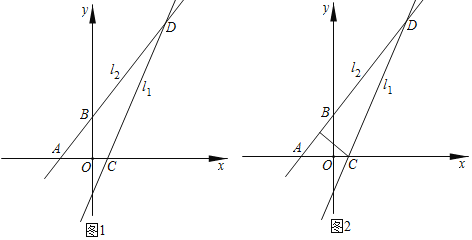
【题目】如图1,在平面直角坐标系中将![]() 向下平移3个单位长度得到直线
向下平移3个单位长度得到直线![]() ,直线
,直线![]() 与x轴交于点C;直线
与x轴交于点C;直线![]() :
:![]() 与x轴、y轴交于A、B两点,且与直线
与x轴、y轴交于A、B两点,且与直线![]() 交于点D.
交于点D.
![]() 填空:点A的坐标为______,点B的坐标为______;
填空:点A的坐标为______,点B的坐标为______;
![]() 直线
直线![]() 的表达式为______;
的表达式为______;
![]() 在直线
在直线![]() 上是否存在点E,使
上是否存在点E,使![]() ?若存在,则求出点E的坐标;若不存在,请说明理由.
?若存在,则求出点E的坐标;若不存在,请说明理由.
![]() 如图2,点P为线段AD上一点
如图2,点P为线段AD上一点![]() 不含端点
不含端点![]() ,连接CP,一动点H从C出发,沿线段CP以每秒1个单位的速度运动到点P,再沿线段PD以每秒
,连接CP,一动点H从C出发,沿线段CP以每秒1个单位的速度运动到点P,再沿线段PD以每秒![]() 个单位的速度运动到点D后停止,求点H在整个运动过程中所用时间最少时点P的坐标.
个单位的速度运动到点D后停止,求点H在整个运动过程中所用时间最少时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电信公司推出甲、乙两种收费方式供手机用户选择:
甲种方式:每月收月租费5元,每分钟通话费为![]() 元;
元;
乙种方式:不收月租费,每分钟通话费为![]() 元;
元;
![]() 请分别写出甲乙两种收费方式每月付费
请分别写出甲乙两种收费方式每月付费![]() 、
、![]() 元
元![]() 与通话时间
与通话时间![]() 分钟
分钟![]() 之间函数表达式;
之间函数表达式;
![]() 如何根据通话时间的多少选择付费方式,请给出你的方案.
如何根据通话时间的多少选择付费方式,请给出你的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第19届亚运会将于2022年在杭州举行,“丝绸细节”助力杭州打动世界.杭州丝绸公司为亚运会设计手工礼品,投入![]() 元钱,若以2条领带和1条丝巾为一份礼品,则刚好可制作600份礼品;若以1条领带和3条丝巾为一份礼品,则刚好可制作400份礼品.
元钱,若以2条领带和1条丝巾为一份礼品,则刚好可制作600份礼品;若以1条领带和3条丝巾为一份礼品,则刚好可制作400份礼品.
(1)若![]() 万元,求领带及丝巾的制作成本是多少?
万元,求领带及丝巾的制作成本是多少?
(2)若用![]() 元钱全部用于制作领带,总共可以制作几条?
元钱全部用于制作领带,总共可以制作几条?
(3)若用![]() 元钱恰好能制作300份其他的礼品,可以选择
元钱恰好能制作300份其他的礼品,可以选择![]() 条领带和
条领带和![]() 条丝巾作为一份礼品(两种都要有),请求出所有可能的
条丝巾作为一份礼品(两种都要有),请求出所有可能的![]() 、
、![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),AB∥CD,猜想∠BPD与∠B.∠D的关系,说明理由.(提示:三角形的内角和等于180°)
①填空或填写理由
解:猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°______
∵AB∥CD,EF∥AB,
∴______∥_____,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠EPD+______=180°
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
②依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B.∠D的关系,并说明理由.

③观察图(3)和(4),已知AB∥CD,直接写出图中的∠BPD与∠B.∠D的关系,不说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),
则称点P′为点P的“k属派生点”.例如:P(1,4)的“2属派生点”为P′(1+2×4,2×1+4),即P′(9,6).
(Ⅰ)点P(﹣2,3)的“3属派生点”P′的坐标为 ;
(Ⅱ)若点P的“5属派生点”P′的坐标为(3,﹣9),求点P的坐标;
(Ⅲ)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com