
【题目】完成下面的证明:
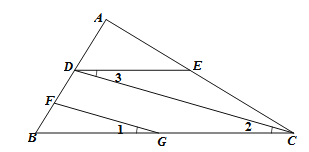
如图,FG//CD,∠1=∠3,∠B=50°,求∠BDE的度数.
解:∵FG//CD (已知)
∴∠2=_________( )
又∵∠1=∠3
∴∠3=∠_________( )
∴BC//__________( )
∴∠B+________=180°( )
又∵∠B=50°
∴∠BDE=130°.
【答案】∠1;两直线平行,同位角相等;∠2;等量代换;DE;内错角相等,两直线平行;∠BDE;两直线平行,同旁内角互补
【解析】
由两直线平行,同位角相等,得到∠2=∠1,再由等式的性质得到∠3=∠2,从而得到BC//DE,再由平行线的性质得到∠B+∠BDE=180°,从而得到结论.
解:∵FG//CD(已知)
∴∠2=∠1(两直线平行,同位角相等)
又∵∠1=∠3,
∴∠3=∠2(等量代换)
∴BC//DE(内错角相等,两直线平行)
∴∠B+∠BDE=180°(两直线平行,同旁内角互补)
又∵∠B=50°
∴∠BDE=130°.
故答案为:∠1;两直线平行,同位角相等;∠2;等量代换;DE;内错角相等,两直线平行;∠BDE;两直线平行,同旁内角互补.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】推理填空
如图:∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F,求证:CE∥DF.请完成下面的解题过程.

解:∵BD平分∠ABC,CE平分∠ACB ( 已知 )
∴∠DBC=![]() ∠_____,∠ECB=
∠_____,∠ECB=![]() ∠_____ ( 角平分线的定义)
∠_____ ( 角平分线的定义)
又∵∠ABC=∠ACB (已知)
∴∠_____=∠_____.
又∵∠_____=∠_____ (已知)
∴∠F=∠_____
∴CE∥DF_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0).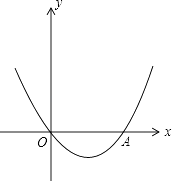
(1)求此抛物线的解析式;
(2)写出顶点坐标及对称轴;
(3)若抛物线上有一点B,且S△OAB=3,求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
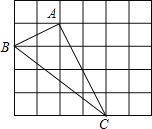
【题目】如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
(1)画线段AD∥BC且使AD=BC,连接CD;
(2)线段AC的长为___,CD的长为___,AD的长为___.
(3)试判断△ACD的形状,并求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D,E分别在AB,AC上,DE∥BC,F是AD上一点,FE的延长线交BC的延长线于点G.求证:
(1)∠EGH>∠ADE;
(2)∠EGH=∠ADE+∠A+∠AEF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,BD是斜边上高动点P从点A出发沿AB边由A向终点B以
,BD是斜边上高动点P从点A出发沿AB边由A向终点B以![]() 的速度匀速移动,动点Q从点B出发沿射线BC以
的速度匀速移动,动点Q从点B出发沿射线BC以![]() 的速度匀速移动,点P、Q同时出发,当点P停止运动,点Q也随之停止
的速度匀速移动,点P、Q同时出发,当点P停止运动,点Q也随之停止![]() 连接AQ,交射线BD于点
连接AQ,交射线BD于点![]() 设点P运动时间为t秒.
设点P运动时间为t秒.
![]() 在运动过程中,
在运动过程中,![]() 的面积始终是
的面积始终是![]() 的面积的2倍,为什么?
的面积的2倍,为什么?
![]() 当点Q在线段BC上运动时,t为何值时,
当点Q在线段BC上运动时,t为何值时,![]() 和
和![]() 相等.
相等.

查看答案和解析>>
科目:初中数学 来源: 题型:
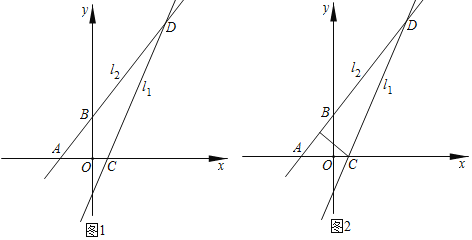
【题目】如图1,在平面直角坐标系中将![]() 向下平移3个单位长度得到直线
向下平移3个单位长度得到直线![]() ,直线
,直线![]() 与x轴交于点C;直线
与x轴交于点C;直线![]() :
:![]() 与x轴、y轴交于A、B两点,且与直线
与x轴、y轴交于A、B两点,且与直线![]() 交于点D.
交于点D.
![]() 填空:点A的坐标为______,点B的坐标为______;
填空:点A的坐标为______,点B的坐标为______;
![]() 直线
直线![]() 的表达式为______;
的表达式为______;
![]() 在直线
在直线![]() 上是否存在点E,使
上是否存在点E,使![]() ?若存在,则求出点E的坐标;若不存在,请说明理由.
?若存在,则求出点E的坐标;若不存在,请说明理由.
![]() 如图2,点P为线段AD上一点
如图2,点P为线段AD上一点![]() 不含端点
不含端点![]() ,连接CP,一动点H从C出发,沿线段CP以每秒1个单位的速度运动到点P,再沿线段PD以每秒
,连接CP,一动点H从C出发,沿线段CP以每秒1个单位的速度运动到点P,再沿线段PD以每秒![]() 个单位的速度运动到点D后停止,求点H在整个运动过程中所用时间最少时点P的坐标.
个单位的速度运动到点D后停止,求点H在整个运动过程中所用时间最少时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com