
【题目】如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0).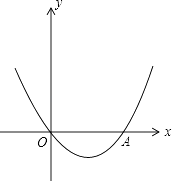
(1)求此抛物线的解析式;
(2)写出顶点坐标及对称轴;
(3)若抛物线上有一点B,且S△OAB=3,求点B的坐标.
【答案】
(1)解:把(0,0),(2,0)代入y=x2+bx+c得
![]() ,
,
解得 ![]() ,
,
∴解析式为y=x2﹣2x
(2)解:∵y=x2﹣2x=(x﹣1)2﹣1,
∴顶点为(1,﹣1)
对称轴为:直线x=1
(3)解:设点B的坐标为(c,d),则
![]() ×2|d|=3,
×2|d|=3,
解得d=3或d=﹣3,
∵顶点纵坐标为﹣1,﹣3<﹣1 (或x2﹣2x=﹣3中,x无解)
∴d=3
∴x2﹣2x=3
解得x1=3,x2=﹣1
∴点B的坐标为(3,3)或(﹣1,3)
【解析】(1)直接把(0,0),(2,0)代入y=x2+bx+c中,列方程组求b、c的值即可抛物线的解析式;
(2)将二次函数解析式写成顶点式,可求顶点坐标及对称轴;
(3)设点B的坐标为(c,d),根据三角形的面积公式 求d的值,再将纵坐标d代入抛物线解析式求c的值,即可求得B点坐标.


科目:初中数学 来源: 题型:
【题目】【探究证明】某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
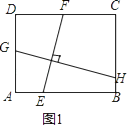
如图1,矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H.求证: ![]() =
= ![]() ;
;
(2)【结论应用】如图2,在满足(1)的条件下,又AM⊥BN,点M,N分别在边BC,CD上,若 ![]() =
= ![]() ,则
,则 ![]() 的值为;
的值为;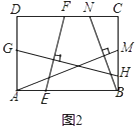
(3)【联系拓展】如图3,四边形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,点M,N分别在边BC,AB上,求 ![]() 的值.
的值.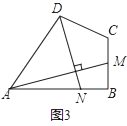
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师在公园道一号购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位:m),解答下列问题:

(1)用含x的代数式表示地面总面积
(2)当x=3时,若铺1m2地砖的平均费用为100元, 那么王老师要将全部地面铺地砖,总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内,现用一注水管沿大容器内壁匀速注水(如图所示),则小水杯内水面的高度h(cm)与注水时间t(min)的函数图象大致为( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形AB1C1D1的边长为1,∠B1=60°;作AD2⊥B1C1于点D2 , 以AD2为一边,做第二个菱形AB2C2D2 , 使∠B2=60°;作AD3⊥B2C2于点D3 , 以AD3为一边做第三个菱形AB3C3D3 , 使∠B3=60°…依此类推,这样做的第n个菱形ABnCnDn的边ADn的长是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明:
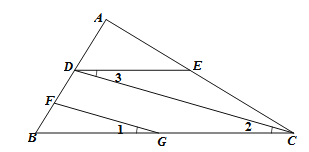
如图,FG//CD,∠1=∠3,∠B=50°,求∠BDE的度数.
解:∵FG//CD (已知)
∴∠2=_________( )
又∵∠1=∠3
∴∠3=∠_________( )
∴BC//__________( )
∴∠B+________=180°( )
又∵∠B=50°
∴∠BDE=130°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与半径为2的⊙O相切于点C,点D,E,F是⊙O上三个点,EF∥AB,若EF=2 ![]() ,则∠EDC的度数为( )
,则∠EDC的度数为( )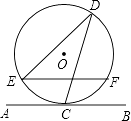
A.60°
B.90°
C.30°
D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB分别与⊙O相切于点A、B,点M在PB上,且OM∥AP,MN⊥AP,垂足为N.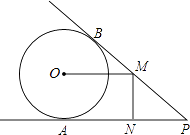
(1)求证:OM=AN;
(2)若⊙O的半径R=3,PA=9,求OM的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com