练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，直线AB与半径为2的⊙O相切于点C，点D，E，F是⊙O上三个点，EF∥AB，若EF=2 ，则∠EDC的度数为（ ）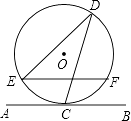

    A.60°
    B.90°
    C.30°
    D.75°

    【答案】C
    【解析】连接OC，与EF交于点G，再连接OE，

    ∵AB为圆O的切线，

    ∴OC⊥AB，

    ∵EF∥AB，

    ∴OC⊥EF，

    ∴EG=FG= EF= ，

    在Rt△OEG中，OE=2，EG= ，

    根据勾股定理得：OG=1，

    ∴∠OEG=30°，

    ∴∠EOG=60°，

    ∵∠EDC与∠EOC都对 ，

    则∠EDC=30°．

    所以答案是：C.

    【考点精析】关于本题考查的切线的性质定理，需要了解切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为了鼓励市民节约用水，某市水费实行分段计费制，每户每月用水量在规定用量及以下的部分收费标准相同，超出规定用量的部分收费标准相同．例如：若规定用量为10吨，每月用水量不超过10吨按1.5元/吨收费，超出10吨的部分按2元/吨收费，则某户居民一个月用水8吨，则应缴水费：8×1.5=12（元）；某户居民一个月用水13吨，则应缴水费：10×1.5+（13﹣10）×2=21（元）．

    表是小明家1至4月份用水量和缴纳水费情况，根据表格提供的数据，回答：

    月份

    一

    二

    三

    四

    用水量（吨）

    6

    7

    12

    15

    水费（元）

    12

    14

    28

    37

    （1）该市规定用水量为　 　吨，规定用量内的收费标准是　 　元/吨，超过部分的收费标准是　 　元/吨．

    （2）若小明家五月份用水20吨，则应缴水费　 　元．

    （3）若小明家六月份应缴水费46元，则六月份他们家的用水量是多少吨？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠DCE=90°，∠DAC=90°，BE⊥AC于B，且DC=EC．

    （1）∠D和∠ECB相等吗？若相等，请说明理由；

    （2）△ADC≌△BCE吗？若全等，请说明理由；

    （3）能否找到与AB+AD相等的线段，并说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=x2+bx+c经过坐标原点，并与x轴交于点A（2，0）．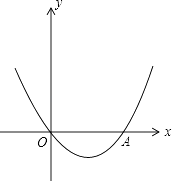

    （1）求此抛物线的解析式；
    （2）写出顶点坐标及对称轴；
    （3）若抛物线上有一点B，且S△OAB=3，求点B的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】△ABC在平面直角坐标系中，且A（-2，1）、B（-3，－2）、C（1，-4）．将其平移后得到△A1B1C1，若A，B的对应点是A1，B1，C的对应点C1的坐标是（3，-1）．

    （1）在平面直角坐标系中画出△ABC和△A1B1C1；

    （2）写出点A1的坐标是_____________，B1坐标是___________；

    （3）此次平移可看作△ABC向________，平移了____________个单位长度，再向_______平移了______个单位长度得到△A1B1C1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点D，E分别在AB，AC上，DE∥BC，F是AD上一点，FE的延长线交BC的延长线于点G.求证：

    (1)∠EGH>∠ADE；

    (2)∠EGH＝∠ADE＋∠A＋∠AEF.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，边长为1的正方形OA1B1C1的两边在坐标轴上，以它的对角线OB1为边作正方形OB1B2C2 ， 再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3 ， 以此类推…、则正方形OB2015B2016C2016的顶点B2016的坐标是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，BC⊥AF于点C，∠A+∠1＝90°．

    （1）求证：AB∥DE；

    （2）如图2，点P从点A出发，沿线段AF运动到点F停止，连接PB，PE．则∠ABP，∠DEP，∠BPE三个角之间具有怎样的数量关系（不考虑点P与点A，D，C重合的情况）？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，Rt△ABC中，∠ABC=90°，以AB为直径作半圆⊙O交AC与点D，点E为BC的中点，连接DE．

    （1）求证：DE是半圆⊙O的切线．
    （2）若∠BAC=30°，DE=2，求AD的长．

    查看答案和解析>>

    同步练习册答案