
����Ŀ����ABC��ƽ��ֱ������ϵ�У���A��-2��1����B��-3����2����C��1��-4��������ƽ�ƺ�õ���A1B1C1����A��B�Ķ�Ӧ����A1��B1��C�Ķ�Ӧ��C1�������ǣ�3��-1����
��1����ƽ��ֱ������ϵ�л�����ABC�͡�A1B1C1��
��2�����A1��������_____________��B1������___________��
��3���˴�ƽ�ƿɿ�����ABC��________��ƽ����____________����λ���ȣ�����_______ƽ����______����λ���ȵõ���A1B1C1��
���𰸡���1����ͼ����������2����0��4������-1��1������3���ϣ�3���ң�2
��������
��1�����õ�A��B��C���������õ���ABC��Ȼ������C���C1��Ĺ�ϵȷ��ƽ�Ƶķ���;��룬���ô�ƽ�ƹ���д��A1��B1�����꣬Ȼ����㼴�ɣ�
��2����ͼ���ɵó�A1��B1�����ꣻ
��3���ɣ�1���е�ƽ�Ƽ��ɵó��𰸣�
��1����ABC����A1B1C1��ͼ��ʾ��
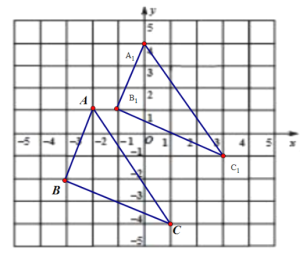
��2����ͼ��֪����A1�������ǣ�0��4����B1�����ǣ�-1��1����
��3���˴�ƽ�ƿɿ�����ABC����ƽ����3����λ���ȣ�������ƽ����2����λ���ȵõ���A1B1C1��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax ![]() +bx+c�����㣨-1,0�����Գ���l��ͼ��ʾ�������н��ۣ���
+bx+c�����㣨-1,0�����Գ���l��ͼ��ʾ�������н��ۣ���
abc ��0����a-b+c=0����2a+c��0����a+b��0������������ȷ�Ľ����ǣ� ��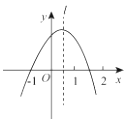
A.�٢�
B.�ڢ�
C.�ڢ�
D.�ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
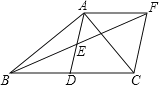
����Ŀ����ͼ������ABC�У���BAC=90�㣬AD�����ߣ�E��AD���е㣬����A��AF��BC��BE���ӳ����ڵ�F������CF��
(1) ��֤��AD=AF��
(2) ����ABC����ʲô����ʱ���ı���ADCF�Ǿ��Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������AB1C1D1�ı߳�Ϊ1����B1=60�㣻��AD2��B1C1�ڵ�D2 �� ��AD2Ϊһ�ߣ����ڶ�������AB2C2D2 �� ʹ��B2=60�㣻��AD3��B2C2�ڵ�D3 �� ��AD3Ϊһ��������������AB3C3D3 �� ʹ��B3=60�㡭�������ƣ��������ĵ�n������ABnCnDn�ı�ADn�ij��� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬AB=5cm��AC=3cm������P�ӵ�B����������BC��1cm/s���ٶ��ƶ������˶���ʱ��Ϊts��
��1����BC�ߵij���
��2������ABPΪֱ��������ʱ����t��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��뾶Ϊ2�ġ�O�����ڵ�C����D��E��F�ǡ�O�������㣬EF��AB����EF=2 ![]() �����EDC�Ķ���Ϊ�� ��
�����EDC�Ķ���Ϊ�� ��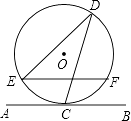
A.60��
B.90��
C.30��
D.75��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ������ϵxOy�У�һ�κ���y=��![]() x+5��ͼ��l1�ֱ���x��y�ύ��A��B���㣬������������ͼ��l2��l1���ڵ�C��m��4����
x+5��ͼ��l1�ֱ���x��y�ύ��A��B���㣬������������ͼ��l2��l1���ڵ�C��m��4����
��1����m��ֵ��l2�Ľ���ʽ��
��2����S��AOC��S��BOC��ֵ��
��3��һ�κ���y=kx+1��ͼ��Ϊl3����11��l2��l3����Χ�������Σ�ֱ��д��k��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������y=��x2+2x+3��x���ཻ��A��B���㣨��A�ڵ�B����ࣩ����y���ཻ�ڵ�C��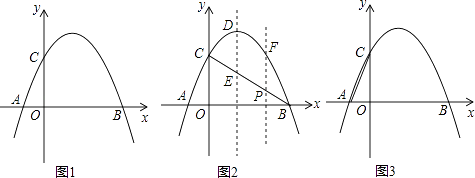
��1��ֱ��д��A��B��C���������������ߵĶԳ��
��2����ͼ2������BC���������ߵĶԳ��ύ�ڵ�E����Pλ�߶�BC�ϵ�һ�����㣬����P��PF��DE���������ڵ�F�����P�ĺ�����Ϊm���ú�m�Ĵ���ʽ��ʾ�߶�PF�ij����������mΪ��ֵʱ���ı���PEDFΪƽ���ı��Σ�
��3����ͼ3������AC����x�����Ƿ���ڵ�Q��ʹ��ACQΪ���������Σ������ڣ��������Q�����꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����С���Һ�ѧУ���ڵصļ�ͼ����֪![]() ��
��![]() ��
��![]() ����CΪOP���е㣬�ش��������⣺
����CΪOP���е㣬�ش��������⣺

��1��ͼ�е�С���Ҿ�����ͬ������Щ�ط���
��2����ͼ��֪������С���Ҷ�ƫ��30������2km�������÷������������ѧУ���̳���ͣ���������С���ҵ�λ�ã�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com