
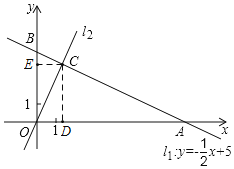
【题目】如图,直角坐标系xOy中,一次函数y=﹣![]() x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
(1)求m的值及l2的解析式;
(2)求S△AOC﹣S△BOC的值;
(3)一次函数y=kx+1的图象为l3,且11,l2,l3不能围成三角形,直接写出k的值.

【答案】(1)m=2,l2的解析式为y=2x;(2)S△AOC﹣S△BOC=15;(3)k的值为![]() 或2或﹣
或2或﹣![]() .
.
【解析】(1)先求得点C的坐标,再运用待定系数法即可得到l2的解析式;
(2)过C作CD⊥AO于D,CE⊥BO于E,则CD=4,CE=2,再根据A(10,0),B(0,5),可得AO=10,BO=5,进而得出S△AOC﹣S△BOC的值;
(3)分三种情况:当l3经过点C(2,4)时,k=![]() ;当l2,l3平行时,k=2;当11,l3平行时,k=﹣
;当l2,l3平行时,k=2;当11,l3平行时,k=﹣![]() ;故k的值为
;故k的值为![]() 或2或﹣
或2或﹣![]() .
.
(1)把C(m,4)代入一次函数y=﹣![]() x+5,可得
x+5,可得
4=﹣![]() m+5,
m+5,
解得m=2,
∴C(2,4),
设l2的解析式为y=ax,则4=2a,
解得a=2,
∴l2的解析式为y=2x;
(2)如图,过C作CD⊥AO于D,CE⊥BO于E,则CD=4,CE=2,
y=﹣![]() x+5,令x=0,则y=5;令y=0,则x=10,
x+5,令x=0,则y=5;令y=0,则x=10,
∴A(10,0),B(0,5),
∴AO=10,BO=5,
∴S△AOC﹣S△BOC=![]() ×10×4﹣
×10×4﹣![]() ×5×2=20﹣5=15;
×5×2=20﹣5=15;
(3)一次函数y=kx+1的图象为l3,且11,l2,l3不能围成三角形,
∴当l3经过点C(2,4)时,k=![]() ;
;
当l2,l3平行时,k=2;
当11,l3平行时,k=﹣![]() ;
;
故k的值为![]() 或2或﹣
或2或﹣![]() .
.


科目:初中数学 来源: 题型:
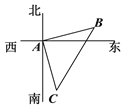
【题目】如图,在一次测绘活动中,某同学站在点A处观测停放于B、C两处的小船,测得船B在点A北偏东75°方向150米处,船C在点A南偏东15°方向120米处,则船B与船C之间的距离为______米(精确到0.1![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
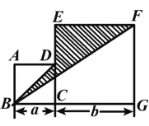
【题目】如图,四边形ABCD与ECGF是两个边长分别为a、b的正方形,
(1)用a、b表示△BGF的面积的代数式S1=
(2)当a=4cm、b=6cm时,求△BGF的面积.
(3)求出阴影部分的面积的代数式S2 (用a、b表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中,且A(-2,1)、B(-3,-2)、C(1,-4).将其平移后得到△A1B1C1,若A,B的对应点是A1,B1,C的对应点C1的坐标是(3,-1).
(1)在平面直角坐标系中画出△ABC和△A1B1C1;
(2)写出点A1的坐标是_____________,B1坐标是___________;
(3)此次平移可看作△ABC向________,平移了____________个单位长度,再向_______平移了______个单位长度得到△A1B1C1.
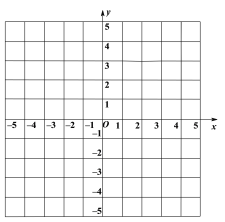
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点B作BE∥AC,在BG上取点E,连接DE交AC的延长线于点F.
(1)求证:DF=EF;
(2)如果AD=2,∠ADC=60°,AC⊥DC于点C,AC=2CF,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2 , 再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3 , 以此类推…、则正方形OB2015B2016C2016的顶点B2016的坐标是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x=﹣3是关于x的方程(k+3)x+2=3x﹣2k的解.
(1)求k的值;
(2)在(1)的条件下,已知线段AB=6cm,点C是直线AB上一点,且BC=kAC,若点D是AC的中点,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:
进价(元/台) | 售价(元/台) | |
电饭煲 | 200 | 250 |
电压锅 | 160 | 200 |
(1)一季度,橱具店购进这两种电器共30台,用去了5600元,并且全部售完,问橱具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50台,且电饭煲的数量不少于电压锅的 ![]() ,问橱具店有哪几种进货方案?并说明理由;
,问橱具店有哪几种进货方案?并说明理由;
(3)在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
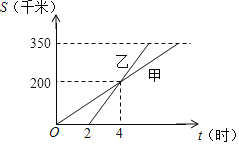
【题目】如图,甲、乙两人利用不同的交通工具,沿同一路线从A地出发到距离A地350千米的B地办事,甲先出发,乙后出发,甲、乙两人距A地的路程和时间的关系如图所示,根据图示提供的信息解答:
![]() 乙比甲晚______小时出发;乙出发______小时后追上甲;
乙比甲晚______小时出发;乙出发______小时后追上甲;
![]() 分别求甲、乙两人离开A地的路程s关于t的函数关系式;
分别求甲、乙两人离开A地的路程s关于t的函数关系式;
![]() 求乙比甲早几小时到达B地?
求乙比甲早几小时到达B地?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com