
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2. 
(1)求证:BC⊥D1E;
(2)若平面BCC1B1与平面BED1所成的锐二面角的大小为 ![]() ,求线段D1E的长度.
,求线段D1E的长度.
【答案】
(1)解:证明:∵底面ABCD和侧面BCC1B1是矩形,∴BC⊥CD,BC⊥CC1,
又∵CD∩CC1=C,∴BC⊥平面DCC1D1,
∵D1E平面DCC1D1,∴BC⊥D1E;
(2)解:由(1)可知BC⊥D1E,
又∵D1E⊥CD,且BC∩CD=C,
∴D1E⊥平面ABCD.
设G为AB的中点,以E为原点,EG,EC,ED1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,如图.
则E(0,0,0),B(1,1,0),C(0,1,0),G(1,0,0).
设D1E=a,则D1(0,0,a),B1(1,2,a).
设平面BED1的一个法向量为 ![]() =(x,y,z),
=(x,y,z),
![]() =(1,1,0),
=(1,1,0), ![]() =(0,0,a),
=(0,0,a),
由 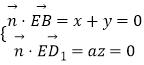 ,令x=1,得
,令x=1,得 ![]() =(1,﹣1,0);
=(1,﹣1,0);
设平面BCC1B1的一个法向量为 ![]() =(x1,y1,z1),
=(x1,y1,z1),
![]() =(1,0,0),
=(1,0,0), ![]() =(﹣1,1,a),
=(﹣1,1,a),
由  ,令z1=1,得
,令z1=1,得 ![]() =(0,﹣a,1).
=(0,﹣a,1).
由平面BCC1B1与平面BED1所成的锐二面角的大小为 ![]() ,
,
得|cos< ![]() >|=|
>|=| ![]() =|cos
=|cos ![]() =
= ![]() ,解得a=1.
,解得a=1.
∴D1E=1.

【解析】(1)由已知底面ABCD和侧面BCC1B1是矩形,可得BC⊥CD,BC⊥CC1 , 由线面垂直的判定可得BC⊥平面DCC1D1 , 进一步得到BC⊥D1E;(2)由(1)可知BC⊥D1E,结合D1E⊥CD,可得D1E⊥平面ABCD.设G为AB的中点,以E为原点,EG,EC,ED1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,求出平面BED1的一个法向量与平面BCC1B1的一个法向量,由平面BCC1B1与平面BED1所成的锐二面角的大小为 ![]() 列式求得a值,则线段D1E的长度可求.
列式求得a值,则线段D1E的长度可求.
【考点精析】通过灵活运用空间中直线与直线之间的位置关系,掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y= ![]() (k>0)的图象与BC边交于点E.
(k>0)的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校准备组织师生共60人,从南靖乘动车前往厦门参加夏令营活动,动车票价格如表所示:(教师按成人票价购买,学生按学生票价购买).
运行区间 | 成人票价(元/张) | 学生票价(元/张) | ||
出发站 | 终点站 | 一等座 | 二等座 | 二等座 |
南靖 | 厦门 | 26 | 22 | 16 |
若师生均购买二等座票,则共需1020元.
(1)参加活动的教师有人,学生有人;
(2)由于部分教师需提早前往做准备工作,这部分教师均购买一等座票,而后续前往的教师和学生均购买二等座票.设提早前往的教师有x人,购买一、二等座票全部费用为y元.
①求y关于x的函数关系式;
②若购买一、二等座票全部费用不多于1032元,则提早前往的教师最多只能多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知过点A(0,1)的椭圆C: ![]() +
+ ![]() =1(a>b>0)的左右焦点分别为F1、F2 , B为椭圆上的任意一点,且
=1(a>b>0)的左右焦点分别为F1、F2 , B为椭圆上的任意一点,且 ![]() |BF1|,|F1F2|,
|BF1|,|F1F2|, ![]() |BF2|成等差数列.
|BF2|成等差数列.
(1)求椭圆C的标准方程;
(2)直线l:y=k(x+2)交椭圆于P,Q两点,若点A始终在以PQ为直径的圆外,求实数k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知F1、F2分别为双曲线C: ![]() =1的左、右焦点,P为双曲线C右支上一点,且|PF1|=2|PF2|,则△PF1F2外接圆的面积为( )
=1的左、右焦点,P为双曲线C右支上一点,且|PF1|=2|PF2|,则△PF1F2外接圆的面积为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣a|+a.
(1)若不等式f(x)≤6的解集为{x|﹣2≤x≤3},求实数a的值;
(2)在(1)的条件下,若存在实数n使f(n)≤m﹣f(﹣n)成立,求实数m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC= ![]() ,点E在AD上,且AE=2ED.
,点E在AD上,且AE=2ED. 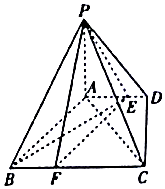
(Ⅰ)已知点F在BC上,且CF=2FB,求证:平面PEF⊥平面PAC;
(Ⅱ)当二面角A﹣PB﹣E的余弦值为多少时,直线PC与平面PAB所成的角为45°?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设椭圆C1: ![]() +
+ ![]() =1(a>b>0),长轴的右端点与抛物线C2:y2=8x的焦点F重合,且椭圆C1的离心率是
=1(a>b>0),长轴的右端点与抛物线C2:y2=8x的焦点F重合,且椭圆C1的离心率是 ![]() .
. 
(1)求椭圆C1的标准方程;
(2)过F作直线l交抛物线C2于A,B两点,过F且与直线l垂直的直线交椭圆C1于另一点C,求△ABC面积的最小值,以及取到最小值时直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com